Предмет: Геометрия,
автор: yus2013
Пожалуйста помогите!!! Площадь боковой поверхности конуса в 3 раза больше площали основания. Найдите обьем конуса, если площадь его осевого сечения равна 8под корнем 2см^2. Ответ:16под корнем2п/3 см^3. Но мне нужно решение, пожалуйста решите его. Заранее спасибо!
Ответы
Автор ответа:
1
S(боковой)=пRl
где l-образующая конуса (можешь почитать в интернете что это)
S(основания)=пR^2
S(боковой)/S(основания)=3=(пRl)/(пR^2)=l/r
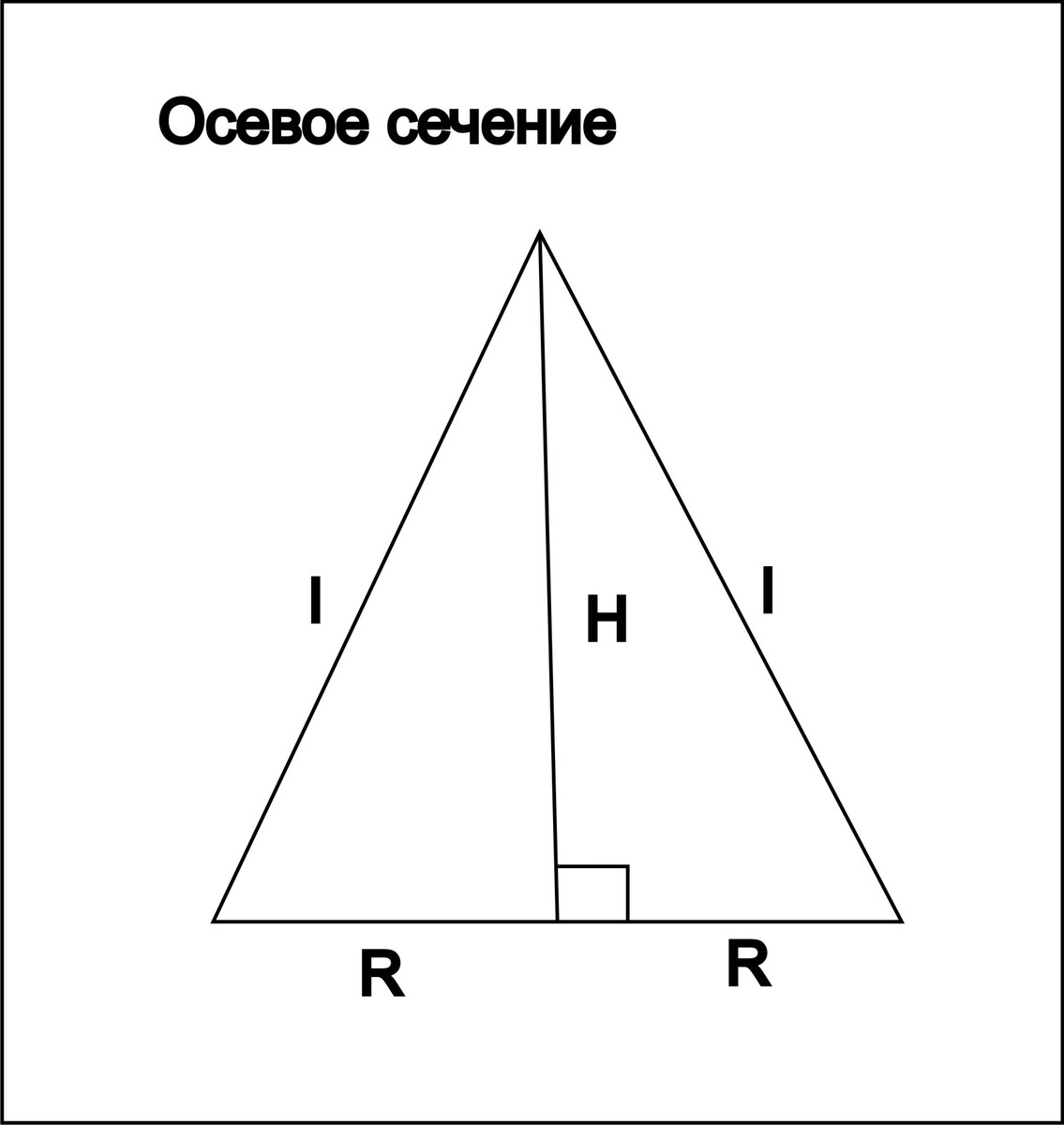
S(осевого сечения)=8sqrt{2}=HR
H-высота конуса
По теореме Пифагора
H^2=l^2-R^2
подставляем в уравнение HR=8sqrt{2}
sqrt{l^2-R^2}*R=8sqrt{2}
подставляем l=3R
получаем R=2
H=4sqrt{2}
V(конуса)=(1/3)*пR^2*H=16sqrt{2}*(п/3)
где l-образующая конуса (можешь почитать в интернете что это)
S(основания)=пR^2
S(боковой)/S(основания)=3=(пRl)/(пR^2)=l/r
S(осевого сечения)=8sqrt{2}=HR
H-высота конуса
По теореме Пифагора
H^2=l^2-R^2
подставляем в уравнение HR=8sqrt{2}
sqrt{l^2-R^2}*R=8sqrt{2}
подставляем l=3R
получаем R=2
H=4sqrt{2}
V(конуса)=(1/3)*пR^2*H=16sqrt{2}*(п/3)
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: totoralol
Предмет: Русский язык,
автор: igorimamov2oz1pz4
Предмет: Қазақ тiлi,
автор: ssbina
Предмет: Математика,
автор: Vlad333222