Предмет: Алгебра,
автор: kirilich99
Докажите , что выражение ...
Приложения:
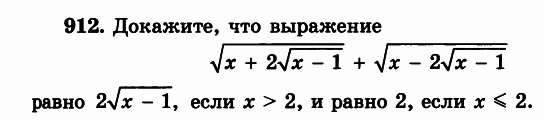
Ответы
Автор ответа:
0
sqrt(x+2sqrt(x-1))+sqrt(x-2sqrt(x-1))=sqrt(x-1+2sqrt(x-1)+1)+sqrt(x-2sqrt(x-1)+1)=sqrt(sqrt(x-1)+1)^2+sqrt(sqrt(x-1)-1)^2=|sqrt(x-1)+1|+|sqrt(x-1)-1|
При x>2 |sqrt(x-1)+1|+|sqrt(x-1)-1|=sqrt(x-1)+1+sqrt(x-1)-1=2*sqrt(x-1)
При x<=2 |sqrt(x-1)+1|+|sqrt(x-1)-1|=sqrt(x-1)+1-sqrt(x-1)+1=2
При x>2 |sqrt(x-1)+1|+|sqrt(x-1)-1|=sqrt(x-1)+1+sqrt(x-1)-1=2*sqrt(x-1)
При x<=2 |sqrt(x-1)+1|+|sqrt(x-1)-1|=sqrt(x-1)+1-sqrt(x-1)+1=2
Автор ответа:
1
ОДЗ: x ∈ [1; ∞) .
√(x+2√(x-1)) +√(x+√(x-1)) =√(x -1+2√(x-1)+1) +√(x-1+√(x-1)+1) =
√(√(x -1) +1)²)+ √(√(x -1) -1)²)= |√(x -1) +1|+|√(x-1) -1|=√(x -1) +1+|√(x-1) -1| .
a) x>2 ;
x-1 >1⇒√(x-1) >1⇒ (x-1) -1>0 то получится
√(x -1) +1+|√(x-1) -1| = √(x -1) +1+ √(x-1) -1 =2√(x-1).
b) 1 ≤x ≤ 2 ;
0≤x-1 ≤ 1 ⇒√(x-1) ≤1⇒ (x-1) -1≤ 0 то получится
√(x -1) +1+|√(x-1) -1| =√(x -1) +1 -√(x-1) +1 = 2 .
√(x+2√(x-1)) +√(x+√(x-1)) =√(x -1+2√(x-1)+1) +√(x-1+√(x-1)+1) =
√(√(x -1) +1)²)+ √(√(x -1) -1)²)= |√(x -1) +1|+|√(x-1) -1|=√(x -1) +1+|√(x-1) -1| .
a) x>2 ;
x-1 >1⇒√(x-1) >1⇒ (x-1) -1>0 то получится
√(x -1) +1+|√(x-1) -1| = √(x -1) +1+ √(x-1) -1 =2√(x-1).
b) 1 ≤x ≤ 2 ;
0≤x-1 ≤ 1 ⇒√(x-1) ≤1⇒ (x-1) -1≤ 0 то получится
√(x -1) +1+|√(x-1) -1| =√(x -1) +1 -√(x-1) +1 = 2 .
Похожие вопросы
Предмет: Українська мова,
автор: annamimonova
Предмет: Русский язык,
автор: угур8
Предмет: Қазақ тiлi,
автор: Ваня2016001
Предмет: Химия,
автор: arukacat
Предмет: Физика,
автор: skinheim