Question

Диагональ делит четырехугольник с периметром 41 см на два треугольника с периметрами 31 см и 40 см. Длина этой диагонали равна...

Answer 1

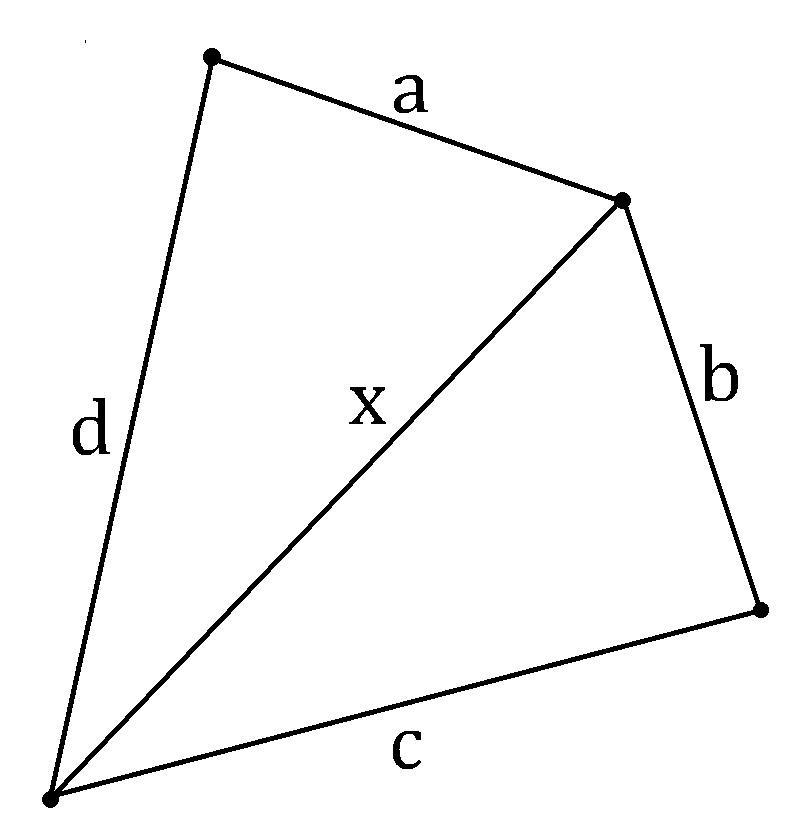
Пусть у четырёхугольника стороны равны a, b, c и d, а его диагональ равна x (см. рис.)

Тогда по условию:

a+b+c+d=41 см; d+a+x=31 см; b+c+x=40 см.

(d+a+x)+(b+c+x)-(a+b+c+d)=31см+40см-41см.

d+a+x+b+c+x-a-b-c-d=30см.

2x=30см |:2;    x=15 см

Ответ: 15см.

Answer 2

Пошаговое объяснение:

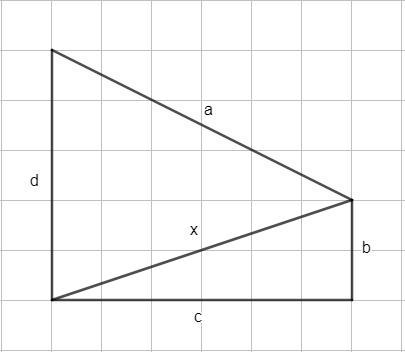
Дано:

x - диагональ

$\tt\displaystyle P_{abcd}=a+b+c+d=41\;cm\\P_{axd}=a+x+d=40\;cm\\P_{bcx}=b+c+x=31\;cm$

P = 40 см                                                P = 31 см

a + x + d = 40                                          b + c + x = 31

(a + d) = 40 - x                                         (b + c) = 31 - x

a + b + c + d = 41

40 - x + 31 - x = 41

71 - 2x = 41

-2x = 41 - 71

-2x = -30

x = -30 : (-2)

x = 15 (см)

Ответ: 15 см - длина диагонали.