Question

При каких по­ло­жи­тель­ных зна­че­ни­ях k пря­мая y=kx-4 имеет с па­ра­бо­лой y=x^2-3x ровно одну общую точку? Най­ди­те ко­ор­ди­на­ты этой точки и по­строй­те дан­ные гра­фи­ки в одной си­сте­ме ко­ор­ди­нат.

Answer 1

Ответ:

Чтобы найти точку пересечения прямой y=k·x-4 с параболой y=x²-3·x приравниваем их выражения и получаем квадратное уравнение:

x²-3·x=k·x-4 ⇔ x²-3·x-k·x+4=0 ⇔ x²-(3+k)·x+4=0.

Если заданные линии имеют только одну общую точку, то дискриминант последнего квадратного уравнения должен быть равен нулю:

D=(-(3+k))²-4·1·4=0.

Решаем уравнение:

(-(3+k))²-4·1·4=0 ⇔ (3+k)²=16 ⇔ 3+k= ±4  ⇔ k= ±4-3.

По условию нужен положительное k, тогда

k= 4-3 = 1.

Значит, уравнение прямой имеет вид:

y=x-4.

Из x²-(3+k)·x+4=0 определим абсциссу точки пересечения:

x²-(3+1)·x+4=0 ⇔ x²-4·x+4=0 ⇔ (x-2)²=0 ⇒ x=2.

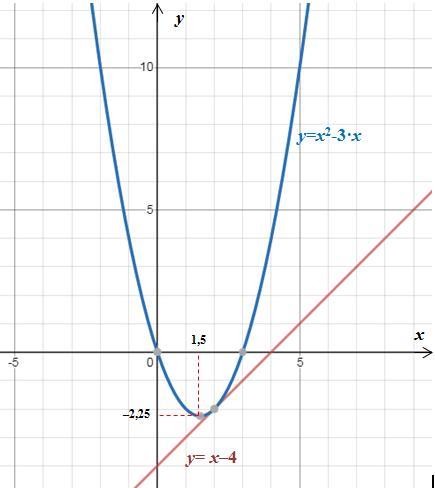
Построим графики данных функций в одной системе координат.

1. График линейной функции y=x-4 прямая, поэтому для построения графика достаточно 2 точки:

1) если х = 0, то у = 0-4 = -4;

2) если х = 4, то у = 4-4 = 0.

Отсюда, прямая проходит через точки (0; -4) и (4; 0).

2. График квадратной функции y=x²-3·x - эта парабола. Для построения графика параболы достаточно 3 точки, одна из которых вершина параболы (красная точка).

Абсциссу вершины параболы y=a•x²+b•x+c определяем по формуле:

$\displaystyle \tt x_{0} =-\dfrac{b}{2 \cdot a} .$

Так как a = 1 и b = -3, то

$\displaystyle \tt x_{0} =-\dfrac{(-3)}{2 \cdot 1} = 1,5.$

Тогда ордината вершины параболы:

y₀=y(x₀) =y(1,5) = 1,5²-3·1,5 = 2,25–4,5= –2,25.

Определяем точки пересечения графика с осью Ох:

f(x)=0 ⇔ x²-3·x=0 ⇔ x·(x-3)=0 ⇔ x₁ = 0, x₂ = 3.

Определяем точку пересечения графика с осью Оу:

f(0) = 0²-3·0 = 0.

Графики функций в приложенном рисунке.