Предмет: Алгебра,
автор: dakota2014
1)лимит
2)область определения
с решением пожалуйста
Приложения:
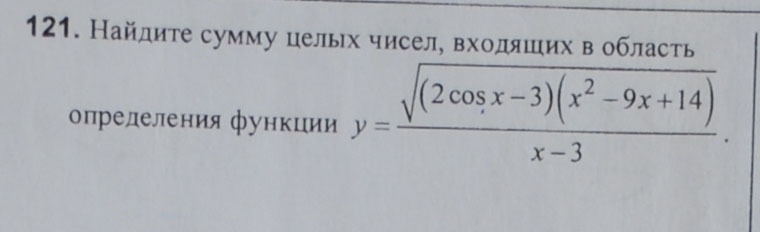
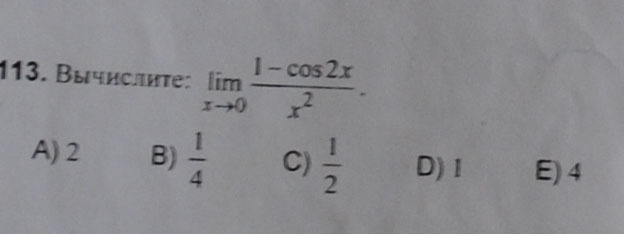
Ответы
Автор ответа:
1
1) Предел

Нашли предел по замечательному пределу.
2) ОДЗ:


 - всегда отрицательное выражение, чтобы произведение было неотрицательным, нужно чтобы второй множитель был неположительным:
- всегда отрицательное выражение, чтобы произведение было неотрицательным, нужно чтобы второй множитель был неположительным:




решением неравенства является:
Возвращаемся к системе:

Ответ: x∈[2;3)U(3;7]
Нашли предел по замечательному пределу.
2) ОДЗ:
решением неравенства является:
Возвращаемся к системе:
Ответ: x∈[2;3)U(3;7]
dakota2014:
самый лучший ответ за все мое пребывание на этом сайте!!!
Похожие вопросы
Предмет: Другие предметы,
автор: Катяcobhac
Предмет: Другие предметы,
автор: Катяcobhac
Предмет: Английский язык,
автор: ksyxa92
Предмет: Обществознание,
автор: Sotoestpopolski