Предмет: Геометрия,
автор: Moymircool
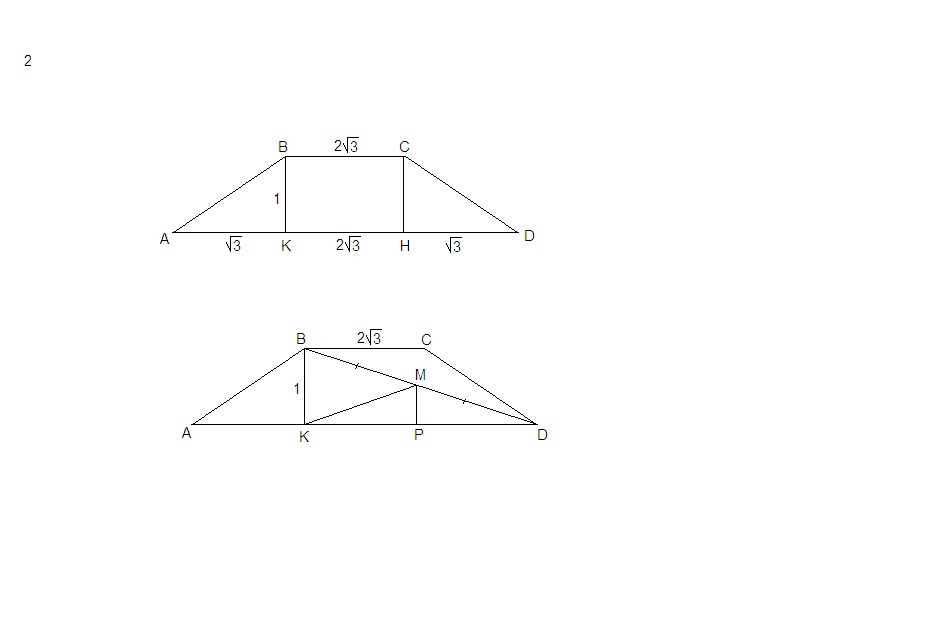
В равнобедренной трапеции ABCD, сторона AD параллельна BC, угол A=30 градусов, высота BK=1 сантиметр, BC=2 корня из 3. Нужно найти площадь трапеции и площадь треугольника KMD - где M середина отрезка BD
Ответы
Автор ответа:
0
ΔАВК: ∠К = 90°, ∠А = 30°, ⇒ АВ = 2ВК = 2 см
по теореме Пифагора АК = √(АВ² - ВК²) = √(4 - 1) = √3 см
Проведем высоту СН.
СН = ВК как высоты одной трапеции, СН ║ ВК как перпендикуляры к одной прямой, значит, КВСН - прямоугольник.
КН = ВС = 2√3 см
ΔАВК = ΔDCH по гипотенузе и катету (AB = CD так трапеция равнобедренная и СН = ВК), значит
AK = HD = 2√3 см
AD = AK + KH + HD = 4√3 см
Sabcd = (AD + BC)/2 · BK = (4√3 + 2√3)/2 · 1 = 3√3 см²
Проведем МР⊥AD. МР - средняя линия треугольника KBD,
МР = ВК/2 = 0,5 см
KD = KH + HD = 3√3 см
Skmd = 1/2 · KD · MP = 0,5 · 3√3 · 0,5 = 3√3/4 см²
по теореме Пифагора АК = √(АВ² - ВК²) = √(4 - 1) = √3 см
Проведем высоту СН.
СН = ВК как высоты одной трапеции, СН ║ ВК как перпендикуляры к одной прямой, значит, КВСН - прямоугольник.
КН = ВС = 2√3 см
ΔАВК = ΔDCH по гипотенузе и катету (AB = CD так трапеция равнобедренная и СН = ВК), значит
AK = HD = 2√3 см
AD = AK + KH + HD = 4√3 см
Sabcd = (AD + BC)/2 · BK = (4√3 + 2√3)/2 · 1 = 3√3 см²
Проведем МР⊥AD. МР - средняя линия треугольника KBD,
МР = ВК/2 = 0,5 см
KD = KH + HD = 3√3 см
Skmd = 1/2 · KD · MP = 0,5 · 3√3 · 0,5 = 3√3/4 см²
Приложения:
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Физика,
автор: dasaresetnak37
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Васильевна