Предмет: Геометрия,
автор: igorDog2014
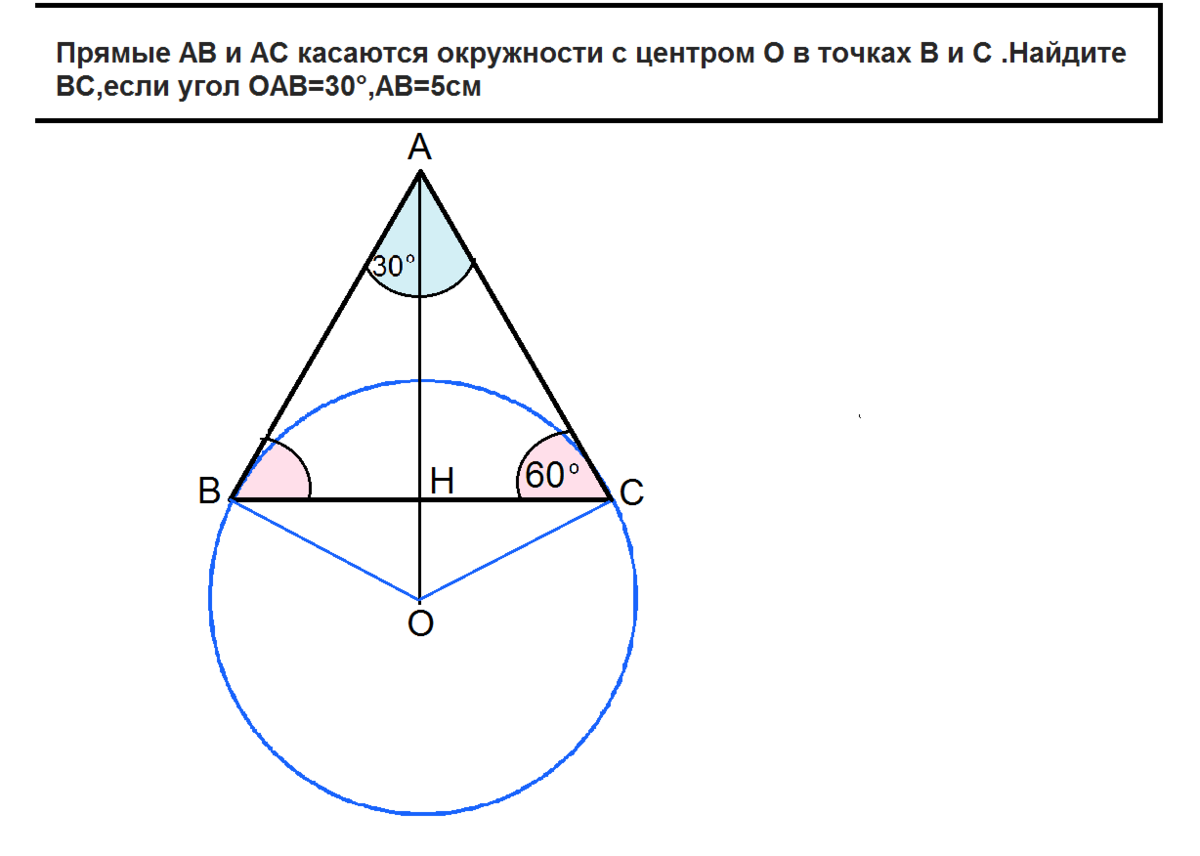
Прямые АВ и АС касаются окружности с центром О в точках В и С .Найдите ВС,если угол ОАВ=30°,АВ=5см
Ответы
Автор ответа:
3
Отрезки касательных, проведенных из одной точки к окружности, равны от этой точки до точек касания.
⇒
Треугольник АВС - равнобедренный.
Треугольники АВО и АСО прямоугольные, т.к. радиус, проведенный к точке касания, перпендикулярен касательной.
Эти треугольники равны по равенству АВ=АС и общей гипотенузе.
Тогда углы ВАО=САО и угол ВАС=2*30°=60°
В равнобедренном треугольнике углы при основании равны. ⇒
углы АВС и АСВ равны (180°-60°):2=60° ⇒
ΔАВС - равносторонний, и ВС=АВ=ВС= 5 см
Ответ: ВС=5 см
---------------
⇒
Треугольник АВС - равнобедренный.
Треугольники АВО и АСО прямоугольные, т.к. радиус, проведенный к точке касания, перпендикулярен касательной.
Эти треугольники равны по равенству АВ=АС и общей гипотенузе.
Тогда углы ВАО=САО и угол ВАС=2*30°=60°
В равнобедренном треугольнике углы при основании равны. ⇒
углы АВС и АСВ равны (180°-60°):2=60° ⇒
ΔАВС - равносторонний, и ВС=АВ=ВС= 5 см
Ответ: ВС=5 см
---------------
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: аля8121
Предмет: Английский язык,
автор: toysse
Предмет: Русский язык,
автор: Resettine
Предмет: География,
автор: antonbukov015