Предмет: Алгебра,
автор: Аноним
Постройте график функции у = ǀх-3ǀ - ǀх+3ǀ и найдите все значения k, при которых прямая у= kх имеет с графиком данной функции ровно одну общую точку.
Аноним:
Это не уравнение.
Вот полное задание:
Постройте график функции у = ǀх-3ǀ - ǀх+3ǀ и найдите все значения k, при которых прямая у= kх имеет с графиком данной функции ровно одну общую точку.
Мне бы хотя бы график построить
Ответы
Автор ответа:
27
Всё дело в том , что под знаком модуля может стоять и положительное число и отрицательное. |x| = x при х ≥
|x| = -x при х меньше 0
первый модуль = 0 при х = 3, второй =0 при х = -3
Вся числовая прямая этими точками разделится на промежутки:
-∞ -3 3 +∞
На каждом промежутке функция будет выглядеть по - своему.
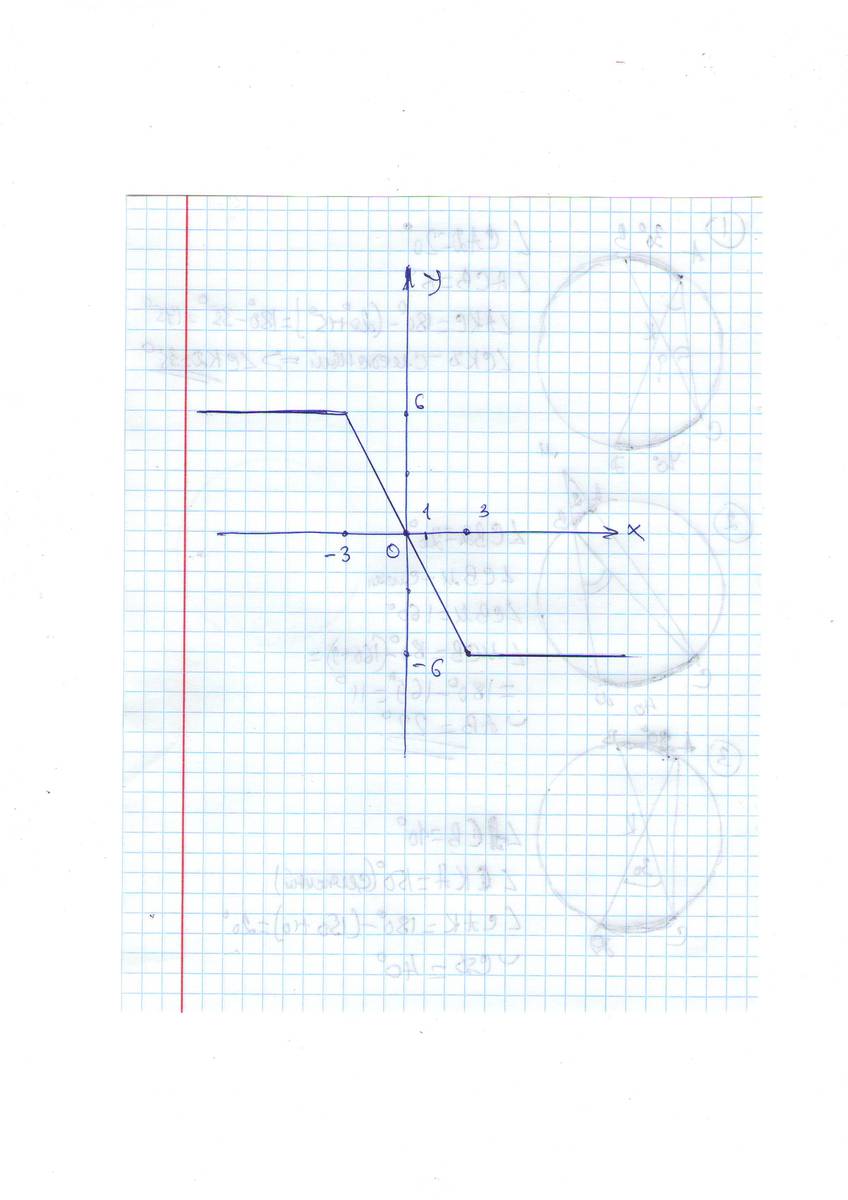
а) (-∞; -3)
у = -(х - 3) + х + 3 = -х +3 +х +3 = 6
у = 6
б) [-3;3]
у = -(х -3) -(х +3) = -х +3 -х -3 = -2х
у = -2х
в) (3; +∞)
у = х - 3-(х +3) = х - 3 - х - 3 = - 6
у = -6
теперь на координатной плоскости надо построить график этой кусочной функции.
Теперь насчёт у = кх. Это прямая, проходящая через начало координат. Чтобы она имела с нашим графиком только одну точку пересечения, надо к выбирать любые, кроме к∈ (0; -2]
|x| = -x при х меньше 0
первый модуль = 0 при х = 3, второй =0 при х = -3
Вся числовая прямая этими точками разделится на промежутки:
-∞ -3 3 +∞
На каждом промежутке функция будет выглядеть по - своему.
а) (-∞; -3)
у = -(х - 3) + х + 3 = -х +3 +х +3 = 6
у = 6
б) [-3;3]
у = -(х -3) -(х +3) = -х +3 -х -3 = -2х
у = -2х
в) (3; +∞)
у = х - 3-(х +3) = х - 3 - х - 3 = - 6
у = -6
теперь на координатной плоскости надо построить график этой кусочной функции.
Теперь насчёт у = кх. Это прямая, проходящая через начало координат. Чтобы она имела с нашим графиком только одну точку пересечения, надо к выбирать любые, кроме к∈ (0; -2]
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: Sonya11111111111gg
Предмет: Английский язык,
автор: mazay2003owbnrq
Предмет: Русский язык,
автор: Znanijavvdgff
Предмет: Русский язык,
автор: lolagrigoreva