Question

В треугольнике АВС проведена биссектриса АМ. Найдите площадь треугольника АВМ, если площадь треугольника АВС равна 40, AB=8, AC=12

Answer 1

В треугольнике АВС проведена биссектриса АМ. Найдите площадь треугольника АВМ, если площадь треугольника АВС равна 40, AB=8, AC=12

По свойству биссектрис: Биссектриса  угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон, имеем:

$\displaystyle \frac{AB}{AC} =\frac{BM}{MC}$

BC ∝ BM + MC

BC ∝ 8 + 12

BC ∝ 20

Площадь треугольника находится по формуле:

S = 1/2 * a * h

S ΔABC = 1/2 * BC * h

S ΔABM = 1/2 * BM * h

Высота одна у обеих фигур, отличается лишь основание. Тогда, зная площадь АВС и отношение оснований - можно найти площадь АВМ:

$\displaystyle \frac{S_A_B_M}{S_A_B_C} =\frac{BM}{BC}\\\\\frac{S_A_B_M}{40} =\frac{8}{20}\\\\\frac{S_A_B_M}{40} =\frac{2}{5}\\\\5S_A_B_M = 80\\\\S_A_B_M = 16$

Ответ: 16 ед².

Answer 2

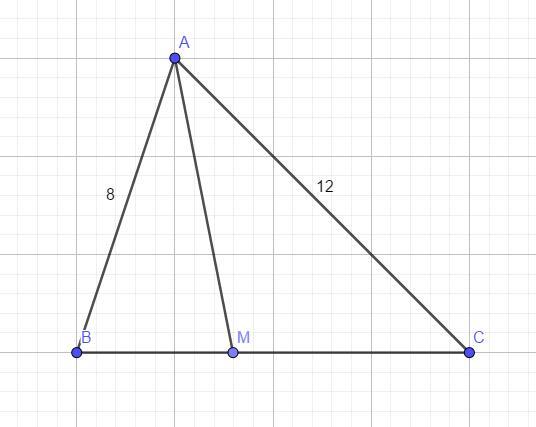
Дано :

ΔАВС.

Отрезок АМ - биссектриса ∠А.

S(ΔАВС) = 40 (ед²).

АВ = 8.

АС = 12.

Найти :

S(ΔABM) = ?

Решение :

Пусть S(ΔABM) = х, тогда S(ΔAMC) = 40 (ед²) - х.

∠ВАМ = ∠МАС - по определению биссектрисы треугольника.

• Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

Отсюда -

$\frac{S(\triangle ABM) }{S(\triangle AMC)} = \frac{AB*AM}{AC*AM} \\\\\frac{S(\triangle ABM) }{S(\triangle AMC)} = \frac{AB}{AC}\\\\\frac{x }{40-x} = \frac{8}{12}\\\\8*(40-x) = 12x\\\\320 - 8x = 12x\\\\320 = 20x\\\\\boxed{x = 16}$

S(ΔABM) = х = 16 (ед²).

Ответ :

16 (ед²).