Question

На расстоянии 10 см от центра шара, радиус которого равен 14 см, проведена плоскость. Вычислите площадь сечения шара этой плоскостью.

Answer 1

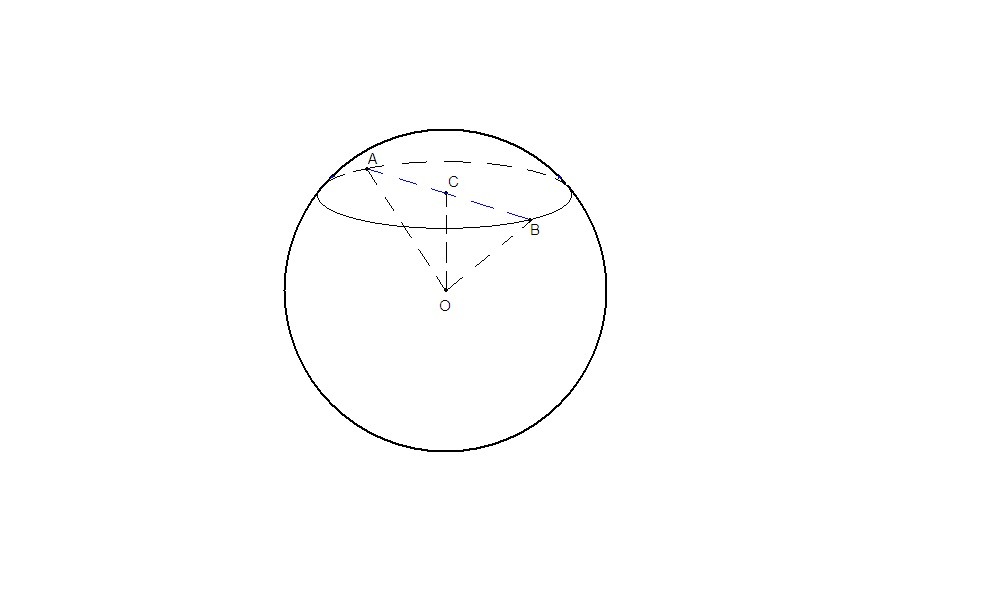
Сечением шара является круг.
О - центр шара, С - центр сечения.
Отрезок, соединяющий центр шара с центром сечения, перпендикулярен плоскости сечения, значит и ОС⊥СВ.
ОС = 10 см, ОВ = 14 см, по теореме Пифагора
СВ = √(ОВ² - ОС²) = √(196 - 100) = √96 см - радиус сечения
Площадь круга:
Sсеч = πr² = π · CB² = 96π см²