Question

Срочно на завтра !!!!!!!!!!!!!!!!!!!!!!!!!!!! За решение всех 5 задач даю 70 баллов
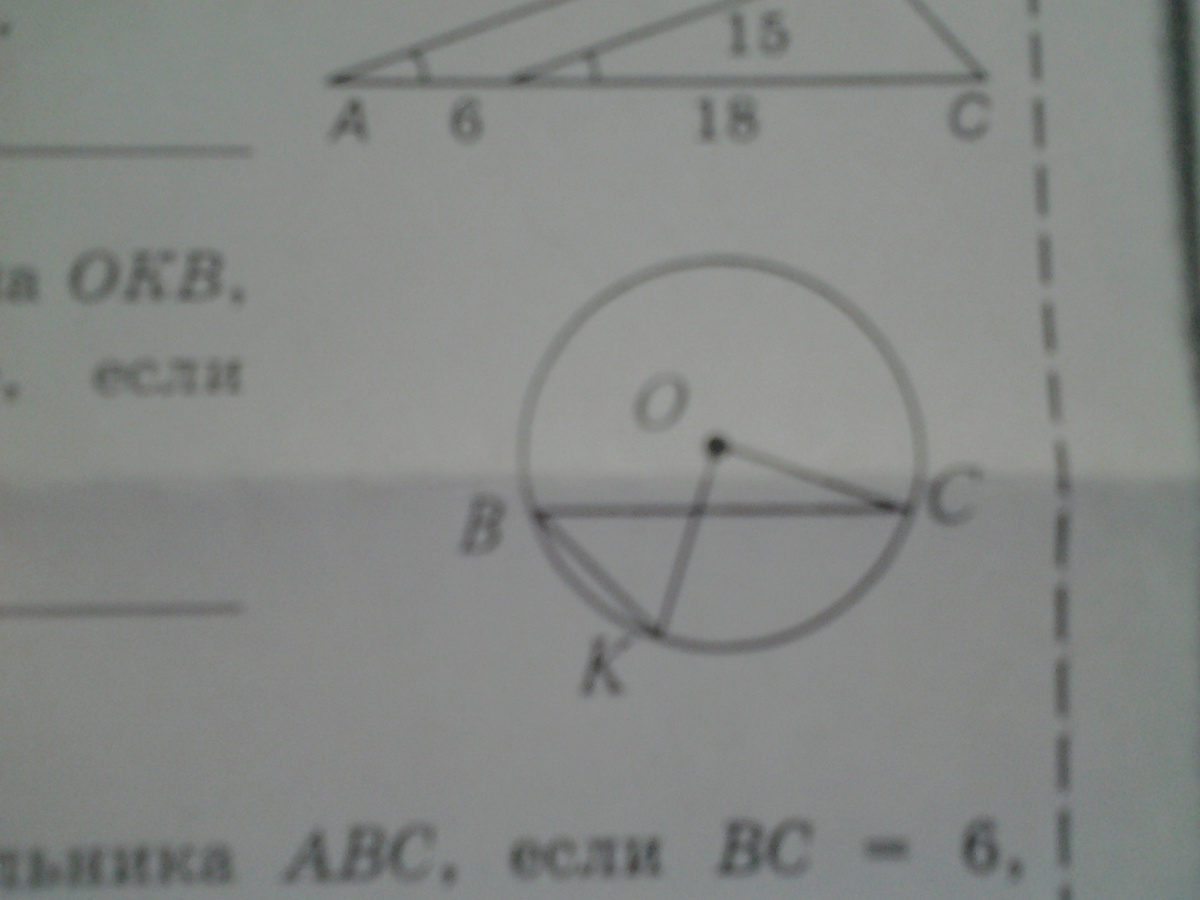
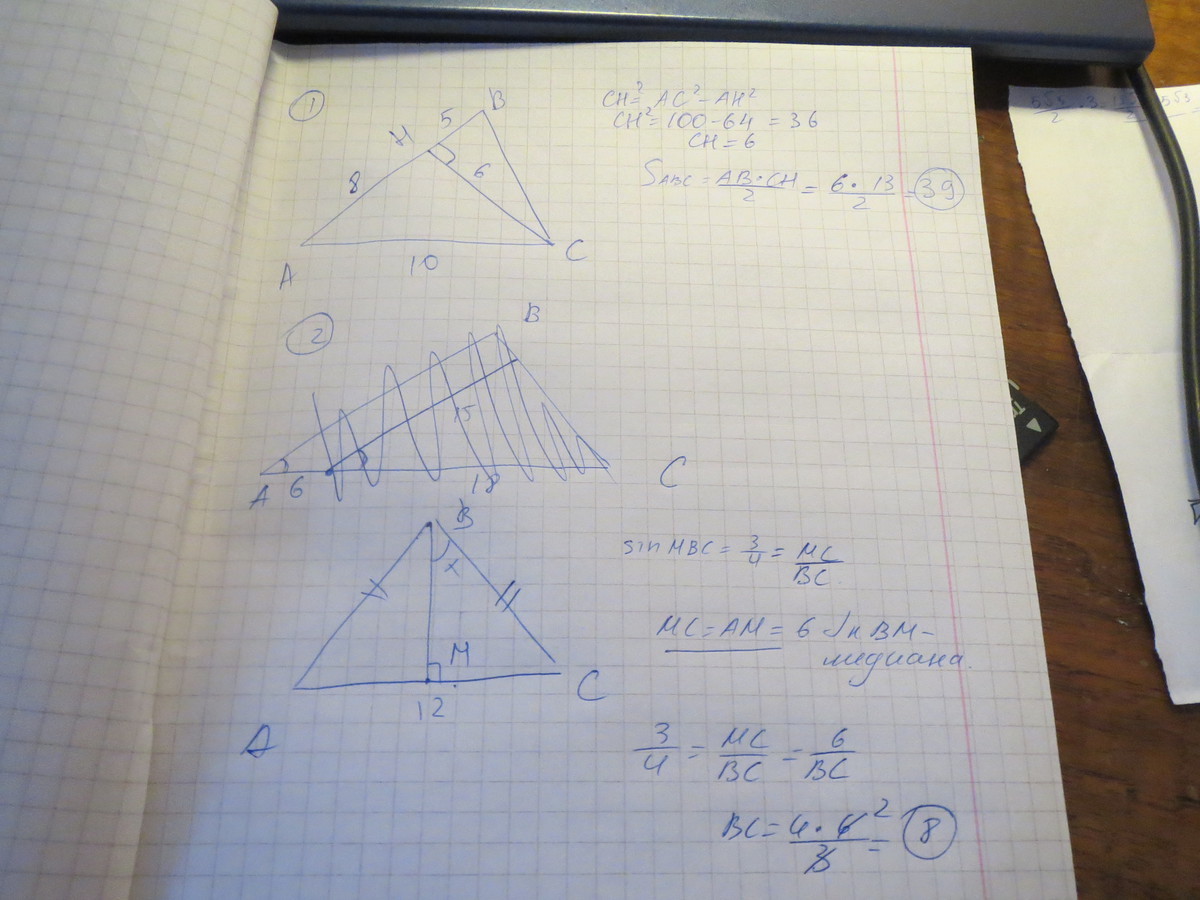
1,Найдите площадь треугольника изображённого нарисунке,


2.В равнобедренном треугольнике ABC с основанием AC равно 12, BM-высота треугольника , синус угла MBC равен 3/4


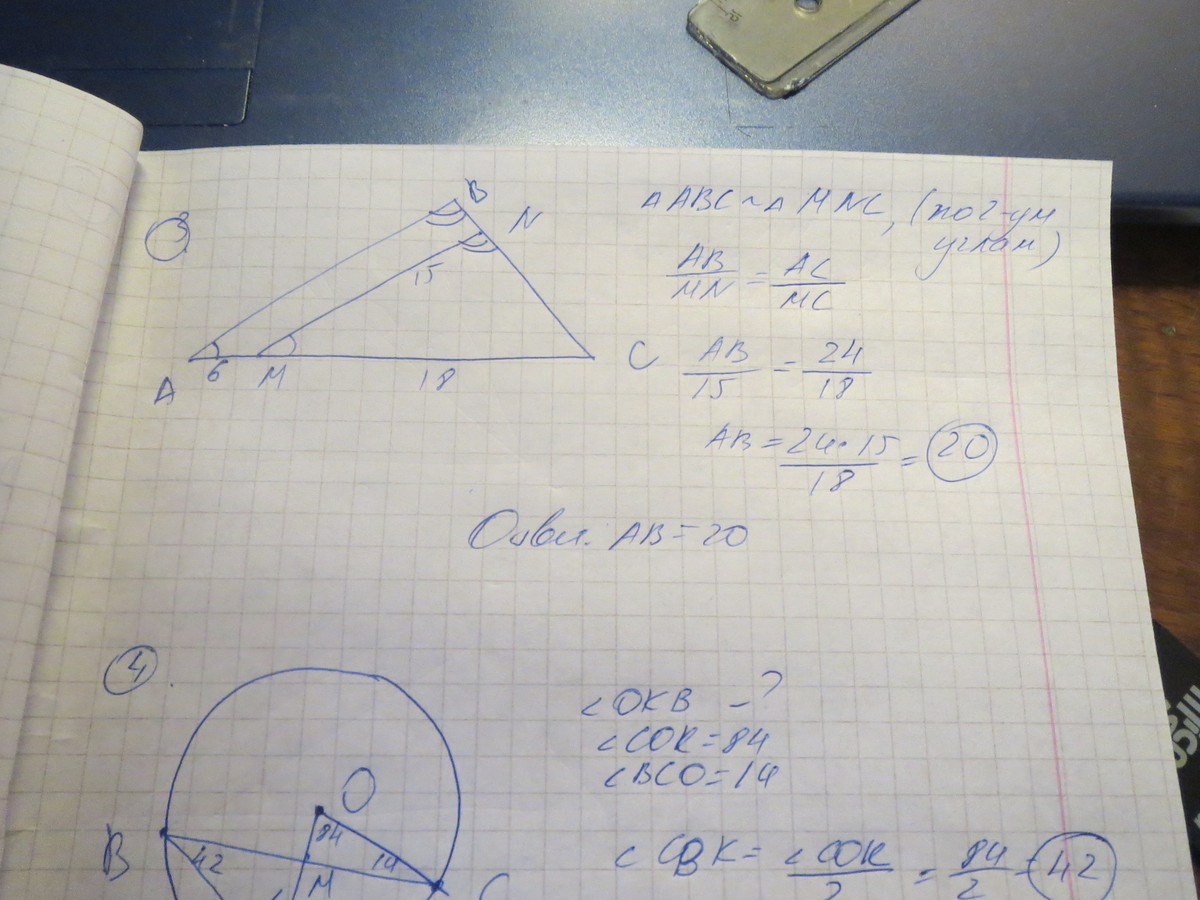
3.Используя данные указания на рисунке, найдите сторону AB


4, Найдите градусную меру угла OKB изображённого на рисунке,если угол COK=84, угол BCO=14


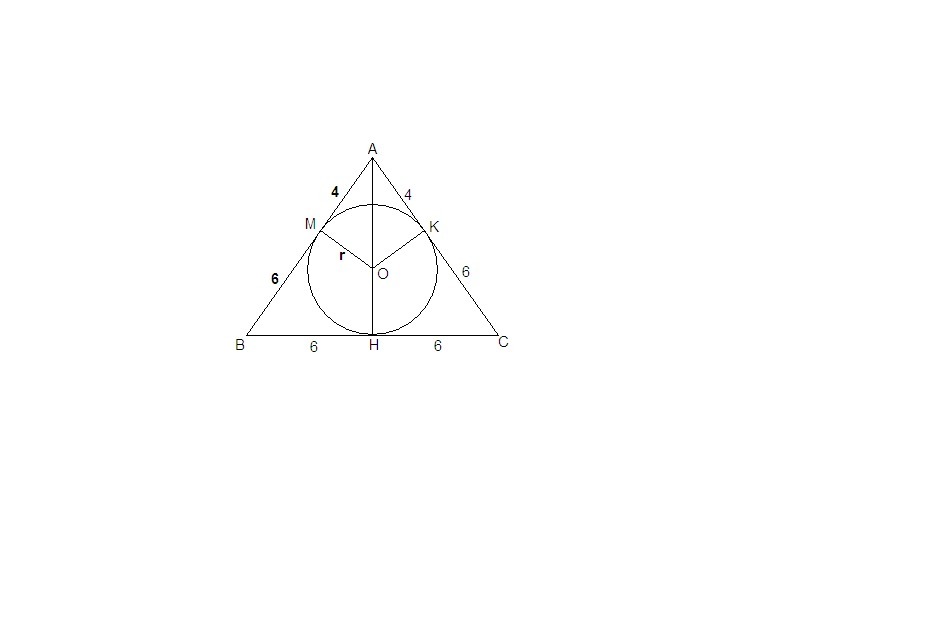
5, В равнобедренный треугольник ABC с основанием BC вписана окружность. Она касается стороны AB в точке M.Найдите радиус окружности,если AM=4 и BM=6.

Answer 1

Задачи 1 - 4 решены Пользователем maSka7 Почетный грамотей
Добавлено решение задачи 5.

5.
Отрезки касательных, проведенных из одной точки, равны.
АК = АМ = 4,
ВН = ВМ = 6.
В равнобедренном треугольнике центр вписанной окружности лежит на высоте (медиане, биссектрисе), проведенной к основанию, поэтому
СН = ВН = 6, и СК = СН = 6 как отрезки касательных.
Pabc = 10+10+12 = 32
p = 32/2 = 16 - полупериметр.
По формуле Герона:
Sabc = √(p·(p - AB)(p - AC)(p - BC)) = √(16 · 6 · 6 · 4)  = 4 · 6 · 2 = 48
Sabc = pr
48 = 16 · r
r = 3