Предмет: Математика,
автор: Stariks
помогите решить 1 интеграл)
Приложения:
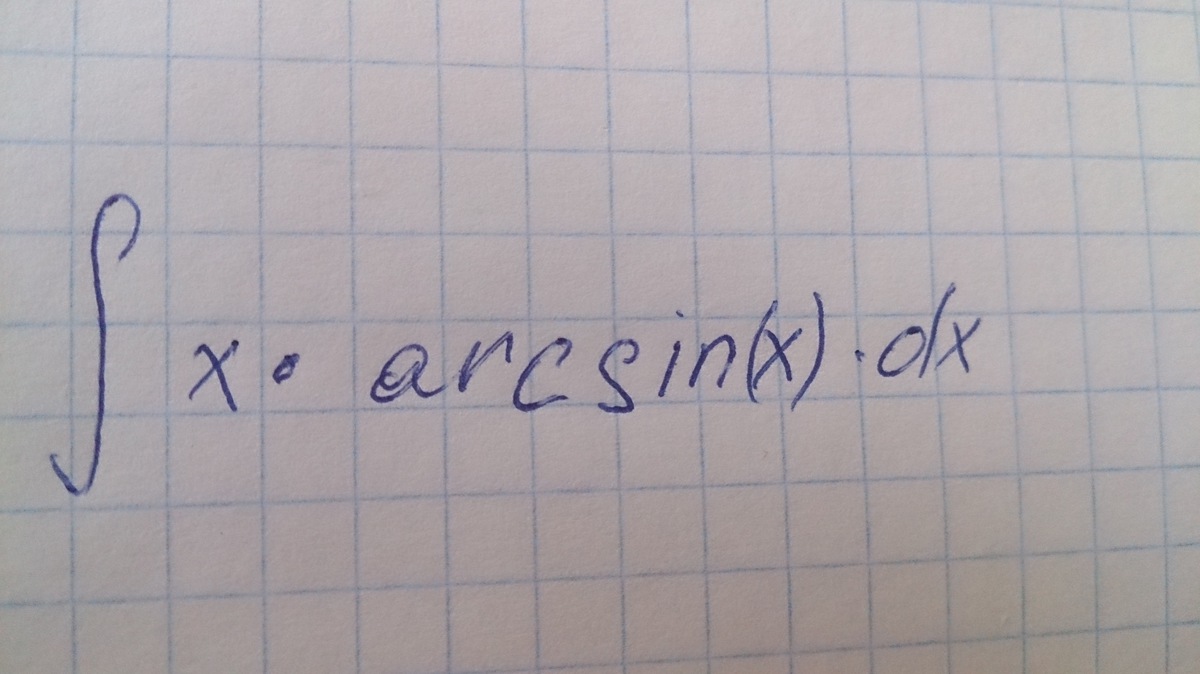
Ответы
Автор ответа:
0
Этот интеграл считается методом интегрирования по частям:
u=arcsinx
du=dx/√(1-х²)
dv=x·dx
v=x²/2

=
Осталось записать по формуле чему равен интеграл в середине ответа
u=arcsinx
du=dx/√(1-х²)
dv=x·dx
v=x²/2
=
Осталось записать по формуле чему равен интеграл в середине ответа
Похожие вопросы
Предмет: Русский язык,
автор: рамиз9
Предмет: Українська мова,
автор: oksanasekretoyfubl
Предмет: Қазақ тiлi,
автор: Zhanel231
Предмет: Информатика,
автор: byrdin2008