Question

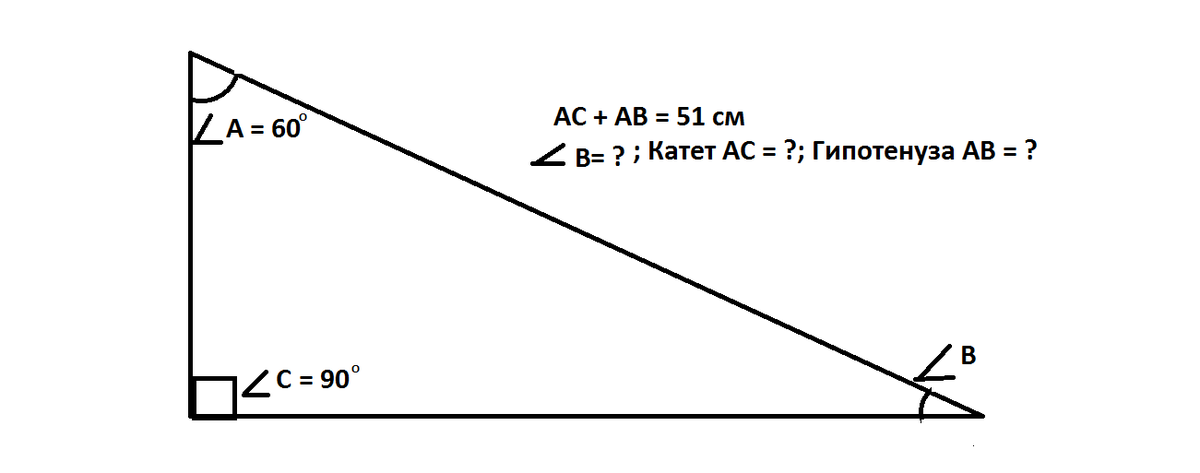
В прямоугольном треугольнике угол С - прямой, угол А - 60 градусов, Сумма сторон АС и АВ равна 51 см. Чему равны угол В, катет АС и гипотенуза АВ?

Answer 1

Угол В=180градусов-60градусов-90градусов=30 градусов. Угол В=30 градусов.
Катет АС равен половине гипотенузы АВ потому что лежит против угла в 30градусов. Известно что сумма АВ и АС равна 51 см. Составим уравнение. Пусть АС - х; тогда АВ - 2х.
Х+2Х=51
3Х=51
Х=51:3
Х=17.
Итак, сторона АС равна 17 см. Значит сторона АВ=17х2=34 см.
Ответ: угол В=30 градусов; сторона АС = 17 см; сторона АВ = 34 см.

Answer 2

Сначала посмотри на рисунок ( внизу):
Внутренние углы треугольника равна $180^{0}$,т.е. угол А + угол В + угол С = $180^{0}$,
Угол А = $60^{0}$, Угол С ( прямой угол ) = $90^{0}$, Угол В = $180^{0}$ - ( $60^{0}$ + $90^{0}$ ) = $30^{0}$.

Сумма сторон АС И АВ = 51см.
Катет АС = Гипотенуза АВ : 2

Катет АС = х, тогда Гипотенуза АВ = 2 × х
Составим уравнение:
х + 2 × х = 51 см
3 × х = 51 см
х = $\frac{51}{3}$ = 17 см - Катет АС
2 × х = 2 × 17 см = 34 см - Гипотенуза АВ

Ответы: угол В = $30^{0}$, Катет АС = 17 см, Гипотенуза АВ = 34 см.