Question

Найдите длину отрезка касательной KM, проведенной к окружности с радиусом равным 1,5 см, если М точка касания и расстояние от центра окружности до точки К равно 2 см.

Answer 1

Касательная КМ в точке касания образует с радиусом окружности угол  = 90 град , т. е. угол КМО=90 ( О --центр окружности ). По теореме Пифагора из ΔКОМ  найдём  КМ :
КО²=КМ²+ОМ²
КМ²=КО²-ОМ²
КМ²=2²-(1,5)²=4-2,25=1,75    КМ=√1,75=1.32
Ответ : 1,32

Answer 2

Вариант решения.
Если из точки вне окружности к ней проведены касательная и секущая, то квадрат длины  отрезка касательной равен произведению всего отрезка секущей на его внешнюю часть.  
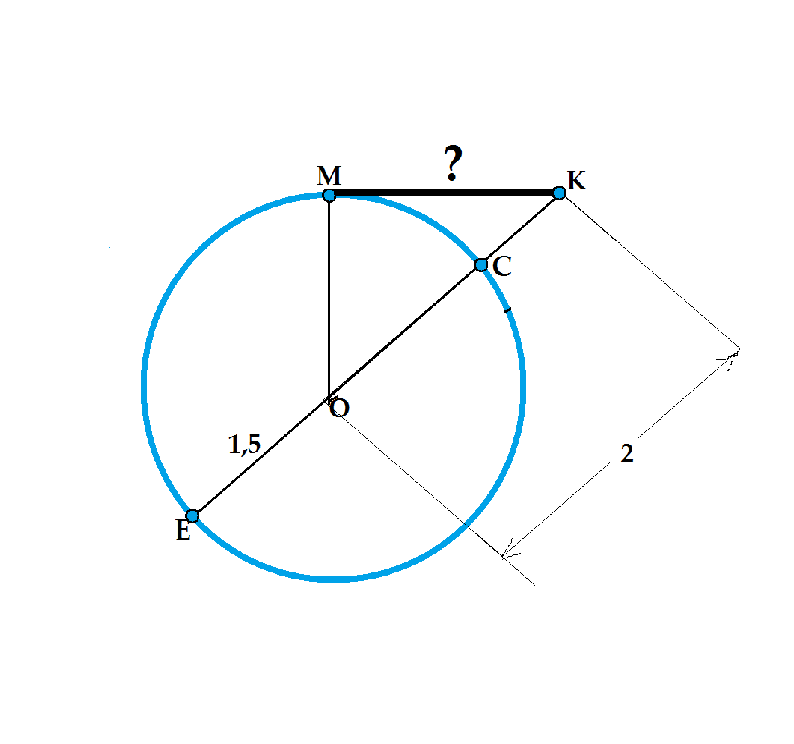
Сделаем рисунок.
Точку пересечения КО с окружностью обозначим С.
Продолжим КО до пересечения с окружностью в точке Е.
КЕ - секущая, МК - отрезок касательной.
КС - внешняя часть секущей.
КМ²=КС·КЕ
КЕ=2+r=3,5
КС=2-r=0,5
КМ²=3,5·0,5=1,75
КМ=√1,75=0,5√7 см