Предмет: Математика,
автор: david82
в треугольник АВС сторона АВ=5 сторона ВС=8 Биссектриса углов А и С пересекаются под углом 45 Найти АС
david82:
пож. да
просто от души
Ответы
Автор ответа:
2
В треугольнике АВС биссектрисы АМ и СН пересекаются под углом 45 градусов. Пусть точка их пересечения будет 45°
Тогда, поскольку угол НОА - внешний при вершине О треугольника СОА, сумма углов, не смежных с ним, равна 45°.
Т,е. угол ОСА+угол САО=45°. Но это полусумма этих углов ( они поделены биссектрисами пополам). ⇒
сумма углов А и С=45°*2=90°,
и тогда
угол В=90°⇒
Δ АВС - прямоугольный, и АС - его гипотенуза.
По т.Пифагора
АС²=АВ²+ВС²=25+64=89
АС=√89
--------------
bzs@
Возможно, в условии ошибка, и АВ=не 5, а 6 (обычно даются такие числа в подобных задачах), и тогда АС=10. Суть решения от этого не меняется.
В прямоугольном треугольнике биссектрисы острых углов всегда пересекаются под углом 45°, а смежный с ним, соответственно, всегда 135°. Это полезно запомнить, т.к. в задачах встречается нередко.
Тогда, поскольку угол НОА - внешний при вершине О треугольника СОА, сумма углов, не смежных с ним, равна 45°.
Т,е. угол ОСА+угол САО=45°. Но это полусумма этих углов ( они поделены биссектрисами пополам). ⇒
сумма углов А и С=45°*2=90°,
и тогда
угол В=90°⇒
Δ АВС - прямоугольный, и АС - его гипотенуза.
По т.Пифагора
АС²=АВ²+ВС²=25+64=89
АС=√89
--------------
bzs@
Возможно, в условии ошибка, и АВ=не 5, а 6 (обычно даются такие числа в подобных задачах), и тогда АС=10. Суть решения от этого не меняется.
В прямоугольном треугольнике биссектрисы острых углов всегда пересекаются под углом 45°, а смежный с ним, соответственно, всегда 135°. Это полезно запомнить, т.к. в задачах встречается нередко.
Приложения:
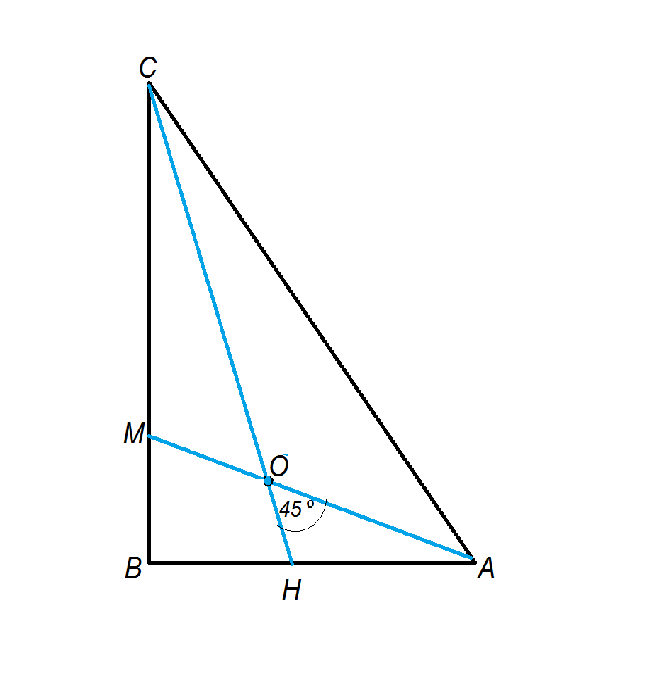
В условии задачи сказано, что биссектрисы ПЕРЕСЕКАЮТСЯ под углом 45*. Там не сказано, что при пересечении они образуют внешний угол в 45*. Решение с подстановкой величины ВНЕШНЕГО угла под величину угла пересечения биссектрис неверно изначально.
Вы несколько заблуждаетесь. Следует просто вспомнить, что "Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине." Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним. (Угол 135 не внешний для треугольника АОС. Он - вертикальный при угле АОС и внешним быть не может. Если не сумела Вас убедить. можно поискать теорему о внешнем угле треугольника в учебнике или интернете.
Мне для понимания условий задачи не нужны теоремы: я читаю и вижу "буковки". Угол между биссектрисами,- это УГОЛ МЕЖДУ БИССЕКТРИСАМИ.
МЕЖДУ, а не СБОКУ.
МЕЖДУ, а не СБОКУ.
Интересный подход к решению задач ). СН и АМ - биссектрисы и при их пересечении образуются 4 (по два равных вертикальных!) угла. Не больше и не меньше. И смежные в сумме дают 180 градусов. Неважно, как Вы нарисуете треугольник. Оба угла - углы между биссектрисами.
Похожие вопросы
Предмет: Другие предметы,
автор: alinaborisfffffrthko
Предмет: Окружающий мир,
автор: dennis19821
Предмет: Русский язык,
автор: rogalevayliay
Предмет: Қазақ тiлi,
автор: Iabox