Предмет: Математика, автор: ga3irovka1337

Постройте график функции y = $\frac{(x^2+6.25)(x-1)}{1-x}$ и определите,при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку

Ответы

Автор ответа: alexbloger

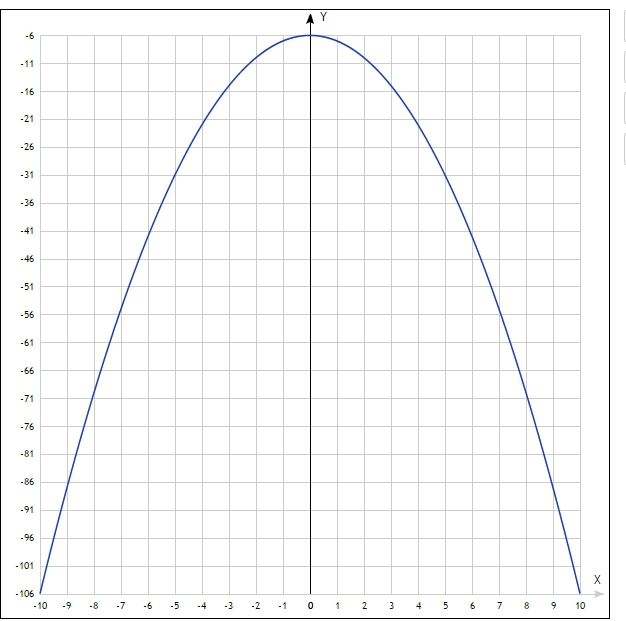
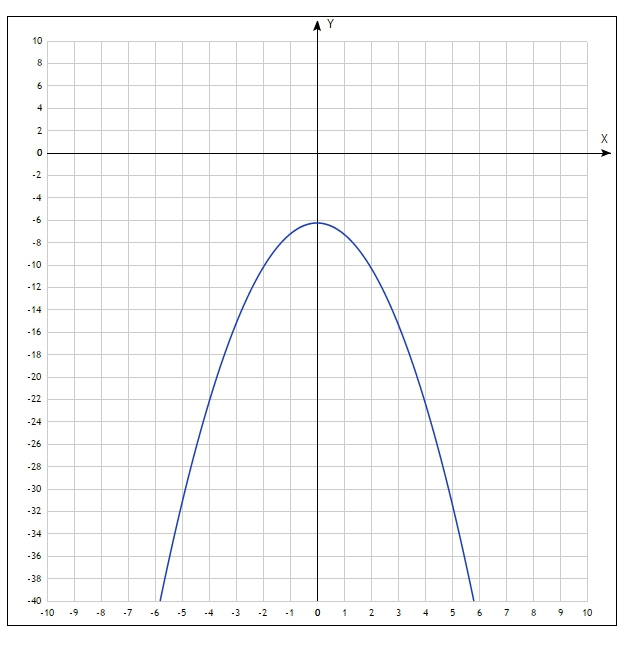
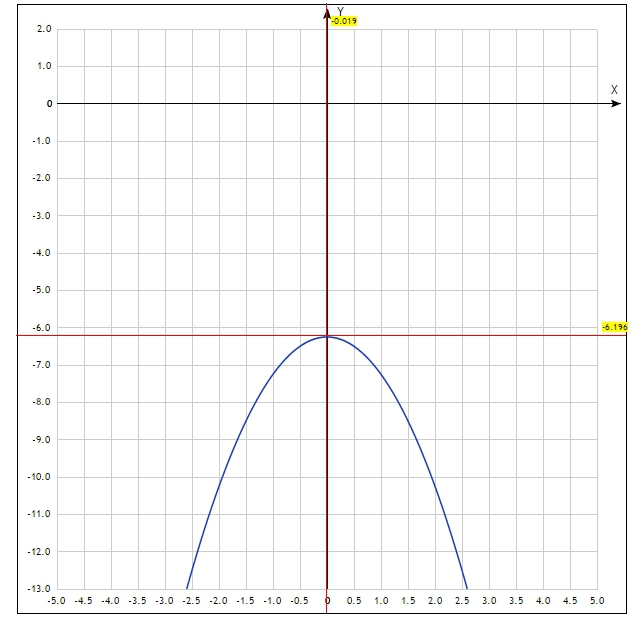
Вот график, в разных масштабах

Приложения:

ga3irovka1337: А решение можно?

alexbloger: а там случайно, не y =kx+b ?

ga3irovka1337: неа,y=kx

alexbloger: y =kx = просто параллельна оси х. в верхней точке и будет значение кх. Приравнять нужно, наверное, обо уравнения.

alexbloger: Точка по графику самая верхняя, это -6.25
Ибо все первое уравнение сокращается до х*х-6.25
А y=kx должно быть как раз -6.25. По графику видно, что по х будет нули, а что не умножишь на ноль, будет ноль.
Если прямая у=kx+b, то тогда у=k*0-6.25, y=-6.25.и тогда прямая будет проходить как раз параллельно оси х, под ней на -6.25 и один раз соприкоснется с графиком, в точке (0,-6.25)

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Українська література, автор: Аноним

Мені потрібен твір на одну із тем:
1.Кобзарі - співці вільного життя.
2.Маруся Богуславка : зрадниця чи патріотка.
3.Устим Кармалюк:розбійник чи захисник народу.
4.За що шанує народ пісні Марусі Чурай.
5.Дума-жанр фольклору,який містить у собі дух епохи незламного покоління.
6."Хоч,здається,не в кайданах,а все ж не на волі".
Бажано з планом;до кожної з тем окрім 1 та 6 потрібно хоча б 2 ЦИТАТИ.

1 год назад

Предмет: Русский язык, автор: NekitTAT

Полный синтаксический разбор предложения! СРОЧНО ПЛ!!!
Я добрался, наконец, до леса, разбил палатку и разжёг костёр.

1 год назад

Предмет: Английский язык, автор: Катя20Денисова

Почему вы выбрали сдавать английский экзамен в этом году? Что вы сделали , чтобы подготовиться к экзамену по английскому языку? Почему многие люди изучают иностранные языки в наше время? Напишите сочинение ( около 20 предложений) СРОЧНО!!!!! НАПИШИТЕ ПЖ СОЧИНЕНИЕ СРОЧНО!!!

1 год назад