Предмет: Математика,
автор: aleksandra5613
помогите найти частные производные первого и второго порядка
Приложения:
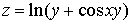
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Английский язык,
автор: Eden186
Предмет: Русский язык,
автор: милана742
Предмет: Русский язык,
автор: NeZnAiKa1o1
Предмет: Химия,
автор: pimopono123
Предмет: Литература,
автор: Gloria23456184