Предмет: Геометрия,
автор: maria7890
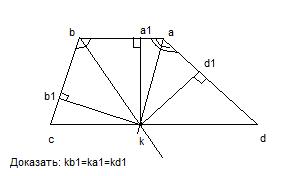
биссектриса углов трапеции abcd пересекаются в точке k лежащей на стороне cd докажите что точка k равноудалена от прямых ab bc и ad
Ответы
Автор ответа:
10
Расстояние от точки до прямой - длина перпендикуляра из этой точки до прямой. Строим kb1, ka1 и kd1. Нужно доказать равенство этих отрезков.
Используем теорему о биссектрисе угла: каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. В нашем случае точка k принадлежит биссектрисе bk неразвернутого угла abc, следовательно, она равноудалена от его сторон:
kb1=ka1
Точка k также принадлежит биссектрисе ak неразвернутого углa bad, значит, она также равноудалена от его сторон:
ka1=kd1. Но ka1=kb1, значит ka1=kb1=kd1.
Используем теорему о биссектрисе угла: каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. В нашем случае точка k принадлежит биссектрисе bk неразвернутого угла abc, следовательно, она равноудалена от его сторон:
kb1=ka1
Точка k также принадлежит биссектрисе ak неразвернутого углa bad, значит, она также равноудалена от его сторон:
ka1=kd1. Но ka1=kb1, значит ka1=kb1=kd1.
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: ilyacc1
Предмет: Окружающий мир,
автор: AlexTyurikov
Предмет: Русский язык,
автор: Лебеда2000
Предмет: Математика,
автор: excalibus
Предмет: Математика,
автор: Аноним