Предмет: Геометрия,
автор: Артур998
Решите номер 13.Есть вложение.
Приложения:
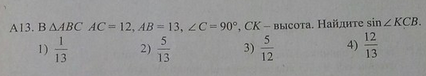
Ответы
Автор ответа:
0
Если BK=x, то AK=(13-х):
Ответ: 2) 5/13
Приложения:

Похожие вопросы
Предмет: Английский язык,
автор: kondra788
Предмет: Английский язык,
автор: дуся57
Предмет: Русский язык,
автор: zelida273
Предмет: Математика,
автор: sanzantosan53
Предмет: Информатика,
автор: usovsasha02