Предмет: Алгебра,
автор: ayka200
100 баллов
срочно докажите плииииииииииииииииииииииииииииз
Приложения:
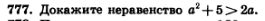
Ответы
Автор ответа:
0
Доказать, что а²+5>2a
Доказательство:
а²+5>2a
a²-2a+5>0
a²-2a+1-1+5>0
(a-1)²+4>0
(a-1)²≥0 для любых а∈(-∞;+∞), т.к. квадрат числа всегда неотрицателен
4 > 0
Следовательно, сумма неотрицательного числа и положительного числа есть число положительное
Значит, (a-1)²+4>0
Следовательно верно и исходное выражение а²+5>2a, т.к. мы совершали тождественные преобразования
Итак, а²+5>2a для любых значений а
Что и требовалось доказать
Доказательство:
а²+5>2a
a²-2a+5>0
a²-2a+1-1+5>0
(a-1)²+4>0
(a-1)²≥0 для любых а∈(-∞;+∞), т.к. квадрат числа всегда неотрицателен
4 > 0
Следовательно, сумма неотрицательного числа и положительного числа есть число положительное
Значит, (a-1)²+4>0
Следовательно верно и исходное выражение а²+5>2a, т.к. мы совершали тождественные преобразования
Итак, а²+5>2a для любых значений а
Что и требовалось доказать
ayka200:
откуда вы берете эти доказательства?????????????????????
из какого сайта??????????????????
будьте добры скажите
Что вы! О каком сайте вы говорите! Это же элементарно.
просто каждый раз у вас ответы с одинаковыми записями и вы так быстро это все печатая присылаете
я добавила 2 пункта неравенства если такие вы "с умом " то решите их
Похожие вопросы
Предмет: Русский язык,
автор: Yoooho111
Предмет: Беларуская мова,
автор: timatim
Предмет: Русский язык,
автор: rygo
Предмет: Английский язык,
автор: ketkvit131456
Предмет: История,
автор: MCMinula11