Question

СРОЧНО. Помогите пожалуйста.

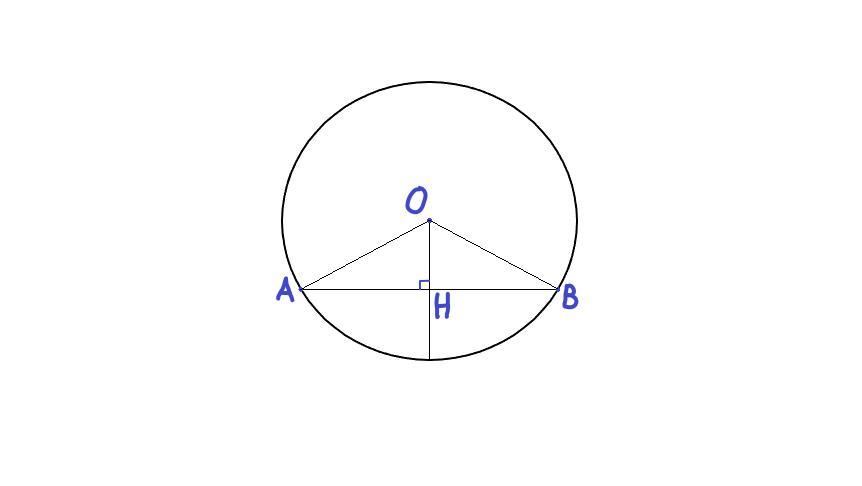
В окружности с центром О через середину радиуса провели хорду АВ, перпендикулярную ему. Докажите, что угол АОВ = 120°

Answer 1

Рассмотрим ΔAOB

Стороны AO и OB являются радиусами окружности, поэтому они будут равны. Отсюда следует, что ΔAOB - равнобедренный ⇒ ∠OAB = ∠OBA

∠AOB = 180° - (∠OAB + ∠OBA) = 180 - 2∠OAB

Рассмотрим ΔAOH - прямоугольный

Точка H - середина радиуса, следовательно OH = 1/2 × OA ⇒ ∠OAB = 30° (так как противолежащий катет равен половине гипотенузы)

∠AOB = 180° - 2∠OAB = 180 - 60 = 120 - доказано