Предмет: Геометрия,
автор: maryamru24
Докажите , что диаметр окружности , проходящий через середину хорды , перпендикулярен хорде .
Ответы
Автор ответа:
24
Доказательство:
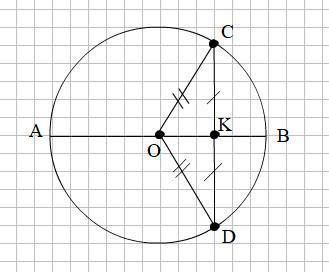
Смотри прикреплённый рисунок.
АВ - диаметр окружности с центром в точке О.
СK = DK - половинки хорды CD.
К - точка пересечения АВ и CD
Соединим концы хорды С и D с центром окружности О.
ΔСОК = Δ DOK по 3-му признаку (СK = DK по условию, ОС = ОD - радиусы окружности, ОК - общая сторона)
Следовательно, ∠СКО = ∠DKO.
Эти углы в сумме составляют развёрнутый ∠СКD = 180°
Следовательно, ∠СКО = ∠DKO = 0,5 ∠СКD = 0,5 · 180° = 90°.
Доказано, что ОК ⊥ CD.
Так как ОК является частью диаметра АВ, то АВ ⊥ CD, что и требовалось доказать.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: мыслюкаксогу2
Предмет: Русский язык,
автор: Baskov2526
Предмет: Русский язык,
автор: BigRussianBoss213
Предмет: Химия,
автор: Indeika
Предмет: Химия,
автор: Лёльке