Question

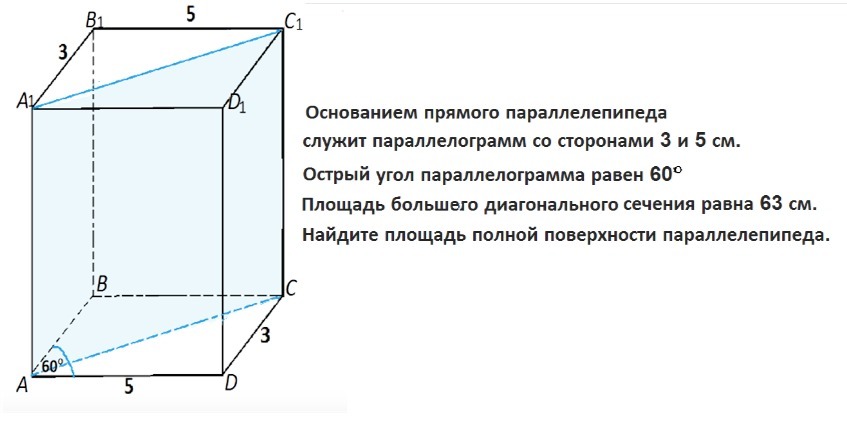
Основанием прямого параллелепипеда служит параллелограмм со сторонами 3 и 5 см. Острый угол параллелограмма равен 60* Площадь большого диагонального сечения равна 63 см. Найдите площадь полной поверхности параллелепипеда.

Answer 1

Площадь полной поверхности параллелепипеда равна сумме площадей двух его оснований и площади боковой поверхности. 
Для ответа на вопрос задачи нужно найти высоту фигуры.
Известна площадь большего диагонального сечения АСС₁А₁.
S АСС₁А₁=AC*СС₁=63 см²
Параллелепипед прямой, рёбра перпендикулярны основанию ⇒
СС₁=высота параллелепипеда.
АС найдем из треугольника АВС по т. косинусов. 
Сумма углов при одной из сторон параллелограмма равна 180°⇒
угол АВС=120°
АС²=АВ²+ВС² -2*AB*BC*cos120°
АС²=9+25- 30*(-1/2)
АС²=49
АС=7см 
Тогда СС1=S AA1C1C:AC=63:7=9 см

Формула площади параллелограмма через стороны и угол между ними

S=a•b•sinα

Площадь двух оснований =2•S(АВСD)=AB•AD•sin60°=15√3

S полная=15√3+2•(3+5)*9=(15√3+144 )cм² или приближённо 170 см²