Предмет: Алгебра,
автор: лоатстчивививи
помогите пожайлусто мне не справится ни как
Приложения:

Ответы
Автор ответа:
0
Решения и ответы прикреплены.
Приложения:

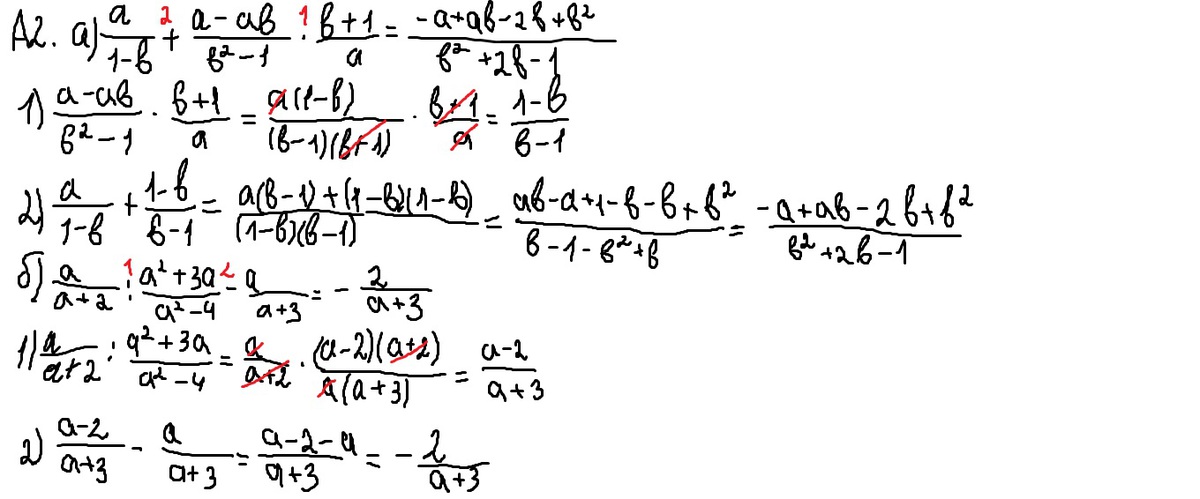
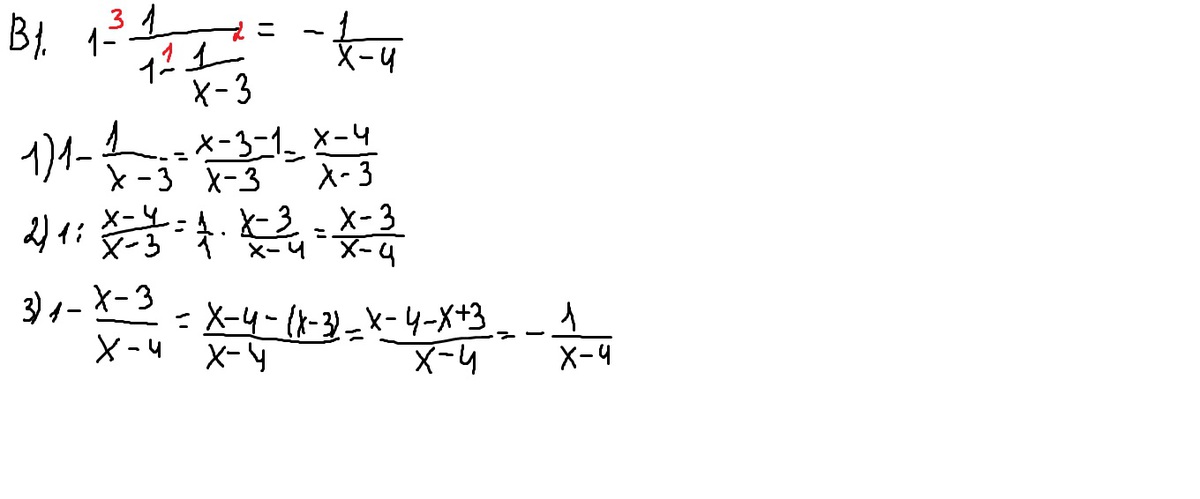
лоатстчивививи:
спасибо огромное
Автор ответа:
0
a)
б)

в)

a)

б)
=


=
б)
в)
a)
б)
=
=
спасибо
Похожие вопросы