Предмет: Алгебра,
автор: YourRescue
Решить поэтапно,ответ [-2:0) and (0;3]
Приложения:
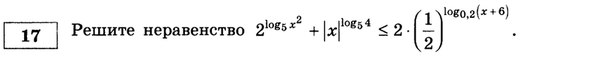
Ответы
Автор ответа:
1
Сначала найдем область допустимых значений.
{x ≠ 0; { x ≠ 0; ⇒ ОДЗ: x ∈ ( - 6; 0) U (0; + ∞)
{x +6 > 0; {x > - 6;
2^(log5_x^2) + [x]^(2*log5_2) ≤ 2* (2^-1) ^(-log5_(x + 6));
Так как [x]^2 = x^2; ⇒
2^(log5_x^2) - (x^2)^log5_2) ≤ 2 * 2^(log5_(x + 6)) ;
Так как по свойству логарифмов a^(logb_c) = c^(logb_a); ⇒
2^(log5_x^2) = (x^2)^(log5_2);
2 * 2^(log5_x^2) ≤ 2 * 2^(log5_(x + 6)) ; /2 >0;
2^(log5_x^2) ≤ 2^(log5_(x +6)) ;
2 > 1; ⇒ log5_x^2 ≤ log5_(x+6);
5 > 1; ⇒ x^2 ≤ x + 6;
x^2 - x - 6 ≤ 0;
(x+ 2)(x - 3) ≤ 0; -2 ≤ х ≤ 3;
+ - +
_________________[-2]___________[3]_____________ x
Сравним с ОДЗ решение неравенства
______(-6)_____________(0)_____________________ х
Получаем при пересечении решения неравенства с одз ответ
х ∈ [-2; 0) U (0; 3]
{x ≠ 0; { x ≠ 0; ⇒ ОДЗ: x ∈ ( - 6; 0) U (0; + ∞)
{x +6 > 0; {x > - 6;
2^(log5_x^2) + [x]^(2*log5_2) ≤ 2* (2^-1) ^(-log5_(x + 6));
Так как [x]^2 = x^2; ⇒
2^(log5_x^2) - (x^2)^log5_2) ≤ 2 * 2^(log5_(x + 6)) ;
Так как по свойству логарифмов a^(logb_c) = c^(logb_a); ⇒
2^(log5_x^2) = (x^2)^(log5_2);
2 * 2^(log5_x^2) ≤ 2 * 2^(log5_(x + 6)) ; /2 >0;
2^(log5_x^2) ≤ 2^(log5_(x +6)) ;
2 > 1; ⇒ log5_x^2 ≤ log5_(x+6);
5 > 1; ⇒ x^2 ≤ x + 6;
x^2 - x - 6 ≤ 0;
(x+ 2)(x - 3) ≤ 0; -2 ≤ х ≤ 3;
+ - +
_________________[-2]___________[3]_____________ x
Сравним с ОДЗ решение неравенства
______(-6)_____________(0)_____________________ х
Получаем при пересечении решения неравенства с одз ответ
х ∈ [-2; 0) U (0; 3]
Похожие вопросы
Предмет: Математика,
автор: lolramem
Предмет: Химия,
автор: lyuba00003
Предмет: Алгебра,
автор: Lisa043
Предмет: Математика,
автор: polina55956
Предмет: Математика,
автор: jackDash209
{x ≠ 0; { x ≠ 0; ⇒ ОДЗ: x ∈ ( - 6; 0) U (0; + ∞)
{x +6 > 0; {x > - 6;
2^(log5_x^2) + [x]^(2*log5_2) ≤ 2* (2^-1) ^(-log5_(x + 6));
Так как [x]^2 = x^2; ⇒
2^(log5_x^2) - (x^2)^log5_2) ≤ 2 * 2^(log5_(x + 6)) ;
Так как по свойству логарифмов a^(logb_c) = c^(logb_a); ⇒
2^(log5_x^2) = (x^2)^(log5_2);
2 * 2^(log5_x^2) ≤ 2 * 2^(log5_(x + 6)) ; /2 >0;
2^(log5_x^2) ≤ 2^(log5_(x +6)) ;
2 > 1; ⇒ log5_x^2 ≤ log5_(x+