Предмет: Алгебра,
автор: nika15s150798
Помогите решить, пожалуйста. Желательно с подробным решением!
Приложения:
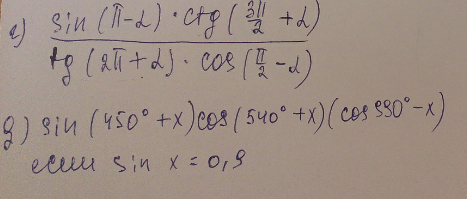
Ответы
Автор ответа:
1
г) sin(π-α) * ctg (3π/2 +α)= sinα*(-tgα) = -1
tg(2π+α)*cos(π/2-α) tgα * sinα
sin(π-α)=-sin(-α)=sinα
cos(π/2-α)=-sin(-α)=sinα
tg(2π+α)=sin(2π+α)= sinα =tgα
cos(2π+α) cosα
ctg(3π/2+α)=ctg(π+π/2+α)=ctg(π/2+α)=cos(π/2+α)=-sinα =-tgα
sin(π/2+α) cosα
д) sin(450°+x) cos(540°+x) cos(990°-x)=cosx * (-cosx)*(-sinx)=cos²x sinx=
=0.19 * 0.9=0.171
sin(450°+x)=sin(360°+90°+x)=sin(90°+x)=cosx
cos(540°+x)=cos(360°+180°+x)=cos(180°+x)=-cosx
cos(990°-x)=cos(1080°-90°-x)=cos(6*360°+(-90°-x))=cos(-90°-x)=
cos(-(90°+x))=cos(90°+x)=-sinx.
sinx=0.9
cos²x=1-sin²x=1-(0.9)²=1-0.81=0.19
tg(2π+α)*cos(π/2-α) tgα * sinα
sin(π-α)=-sin(-α)=sinα
cos(π/2-α)=-sin(-α)=sinα
tg(2π+α)=sin(2π+α)= sinα =tgα
cos(2π+α) cosα
ctg(3π/2+α)=ctg(π+π/2+α)=ctg(π/2+α)=cos(π/2+α)=-sinα =-tgα
sin(π/2+α) cosα
д) sin(450°+x) cos(540°+x) cos(990°-x)=cosx * (-cosx)*(-sinx)=cos²x sinx=
=0.19 * 0.9=0.171
sin(450°+x)=sin(360°+90°+x)=sin(90°+x)=cosx
cos(540°+x)=cos(360°+180°+x)=cos(180°+x)=-cosx
cos(990°-x)=cos(1080°-90°-x)=cos(6*360°+(-90°-x))=cos(-90°-x)=
cos(-(90°+x))=cos(90°+x)=-sinx.
sinx=0.9
cos²x=1-sin²x=1-(0.9)²=1-0.81=0.19
Похожие вопросы
Предмет: Алгебра,
автор: ahrigodxx
Предмет: Немецкий язык,
автор: ilia29865489
Предмет: Українська мова,
автор: Аноним
Предмет: Математика,
автор: DIanaTroeVa
Предмет: Русский язык,
автор: pola89