Предмет: Геометрия,
автор: Adelya8Miller
Три круга (площадь каждого из них равна S) касаются друг друга. Найдите площадь круга, который внутренним образом касается трех данных кругов.
Нужно подробное решение, ответ: S(7 − 4√3) / 3.
Приложения:
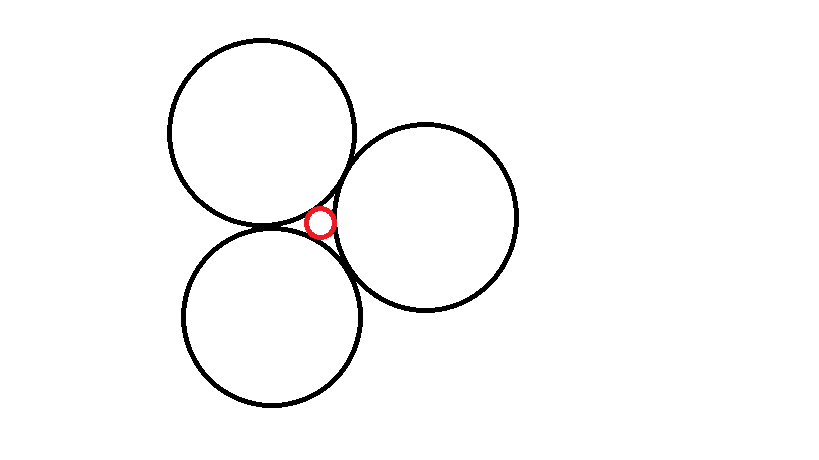
Ответы
Автор ответа:
9
По сути дела надо рассматривать Δ , образованный центрами трёх кругов.Этот треугольник равносторонний со стороной 2R . Центр четвёртого круга - это точка пересечения медиан. Медианы, пересекаясь, делятся в отношении 1:2. Вот этим и будем пользоваться.
Ищем медиану. по т. Пифагора. m² = (2R)² - R²
m² = 4R² - R²
m² =3R²
m = R√3
теперь ищем радиус нового (четвёртого) круга . Этот радиус = 2/3 m + R= =2/3·R√3 + R= 2R/3√3 + R. Ищем площадь. S1 = π(2R/3√3 + R)²= π R²(2 + 3√3)/3√3)²
Осталось выразить R через S. Зная, что S = π R², получим R² = (S/ π)
S1 = S( 7 - 4√3)/3
Ищем медиану. по т. Пифагора. m² = (2R)² - R²
m² = 4R² - R²
m² =3R²
m = R√3
теперь ищем радиус нового (четвёртого) круга . Этот радиус = 2/3 m + R= =2/3·R√3 + R= 2R/3√3 + R. Ищем площадь. S1 = π(2R/3√3 + R)²= π R²(2 + 3√3)/3√3)²
Осталось выразить R через S. Зная, что S = π R², получим R² = (S/ π)
S1 = S( 7 - 4√3)/3
или я чего-то не понимаю
Я нашёл свой косяк. Всё получается. Посмотри Новый радиус(четвёртого круга). Он = (2R√3)/3 + R
Похожие вопросы
Предмет: Математика,
автор: александра20063
Предмет: Информатика,
автор: ekaterinazaruck
Предмет: Математика,
автор: привет888
Предмет: Алгебра,
автор: doodlik20
возможно, в ответе опечатка