Question

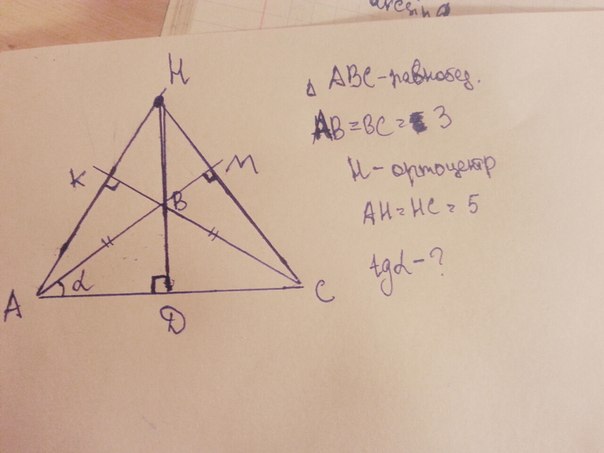
Треугольник ABC равнобедренный тупоугольный
Найти угол tga , на рисунке обозначен

Answer 1

<BAD=a;
<BHA=a;
<ABK = 2a
AH=AK+KH=AB*sin(2a)+KB/tg(a)=AB*sin(2a)+AB*cos(2a)/tg(a)
AH=AB*sin(2a)+AB*cos(2a)/tg(a)
AH=AB*(sin(2a)+cos(2a)/tg(a))
AH=AB*(2sin(a)*cos(a)+(cos^2-sin^2(a))*cos(a)/sin(a))
5*sin(a)=3*(2sin^2(a)*cos(a)+(cos^2-sin^2(a))*cos(a))
5*sin(a)=3*(sin^2(a)*cos(a)+cos^2(a)*cos(a))
5*sin(a)=3*(sin^2(a)+cos^2(a))*cos(a)
5*sin(a)=3*cos(a)
tg(a)=sin(a)/cos(a)=3/5 - это ответ