Предмет: Математика,
автор: freaker230
Найти интервал сходимости степенного ряда и исследовать его на концах
Приложения:
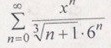
Ответы
Автор ответа:
2
тогда
Интервал сходимости (-6;6)
При х=-6
Получим знакочередующийся ряд, который сходится по признаку Лейбница
При х=6 ряд расходится по интегральному признаку.
Похожие вопросы
Предмет: Математика,
автор: veravera75737
Предмет: Литература,
автор: Angelina2122
Предмет: Математика,
автор: sun1002
Предмет: Физика,
автор: malikaainuraoxuilg
Предмет: Математика,
автор: mimidasha66