Предмет: Геометрия,
автор: кит23445
ПОЖАЛУЙСТА ПОМОГИТЕ! ООООЧЕНЬ НУЖНО!
В основании пирамиды SABC лежит прямоугольный треугольник с катетами AC=8, BC=6, высота пирамиды равна 4. Если вершина пирамиды S проектируется в середину
гипотенузы AB, то площадь боковой поверхности равна.
Ответы
Автор ответа:
5
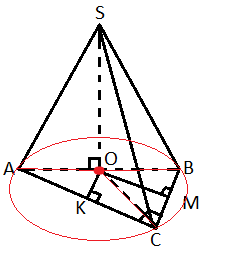
все мои буквы смотри на рисунке в приложении
итак
найдем АВ по тео Пифагора
АВ²=6²+8²=100
АВ=√100=10
АО = ОВ т.к. точка О - это середина описанной окружности т.к треугольник АВС прямоугольный, а АВ - гипотинуза
делаем вывод, что треугольник АОС и треугольник ВОС - равнобедренный, а это значит, что высота, проведенная к основанию, будет падать на середину основания
найдем высоту АОС, чтобы найти SK
5²=4²+ОК²
ОК²=9
OK=3
найдем SK²=OK²+SO²
SK²=3²+4²=25
SK=5
найдем половину боковой грани SAC (эта половина есть треугольник SKC)
она будет равна 10
значит вся грань 10*2=20
так же находим грань SBС
ОM будет равна 4
SM будет равна 4√2
половина площади SBC = 6√2
вся грань 12√2
S ABC = 1/2 * 8 * 6 = 24
половина SAB = 1/2 * 4 * 5 = 10
вся SAB = 20
теперь просто складываем
S полное = 20 + 24 +12√2 + 20 = 64+12√2
итак
найдем АВ по тео Пифагора
АВ²=6²+8²=100
АВ=√100=10
АО = ОВ т.к. точка О - это середина описанной окружности т.к треугольник АВС прямоугольный, а АВ - гипотинуза
делаем вывод, что треугольник АОС и треугольник ВОС - равнобедренный, а это значит, что высота, проведенная к основанию, будет падать на середину основания
найдем высоту АОС, чтобы найти SK
5²=4²+ОК²
ОК²=9
OK=3
найдем SK²=OK²+SO²
SK²=3²+4²=25
SK=5
найдем половину боковой грани SAC (эта половина есть треугольник SKC)
она будет равна 10
значит вся грань 10*2=20
так же находим грань SBС
ОM будет равна 4
SM будет равна 4√2
половина площади SBC = 6√2
вся грань 12√2
S ABC = 1/2 * 8 * 6 = 24
половина SAB = 1/2 * 4 * 5 = 10
вся SAB = 20
теперь просто складываем
S полное = 20 + 24 +12√2 + 20 = 64+12√2
Приложения:
Похожие вопросы
Предмет: Математика,
автор: depper618
Предмет: Математика,
автор: 787878ga
Предмет: Обществознание,
автор: OsKar2003eeee
Предмет: Русский язык,
автор: LikaKotikova
Предмет: Математика,
автор: radmira94