Предмет: Геометрия,
автор: SegaBW
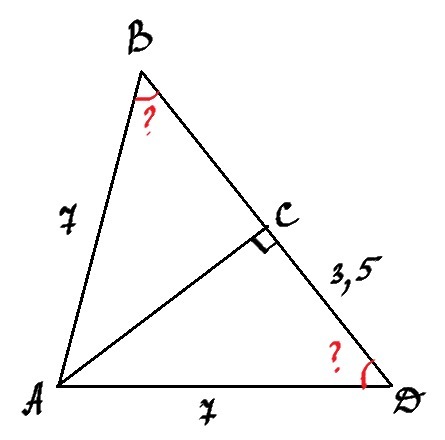
треугольник ABD AB=7cм,AD=7см,CD=3,5см угол С=90 градусов,AC биссектриса найти угол B,угол D
(2 задача)
Приложения:

polechkaluna:
некорректно как-то. у вас в учебнике или где-то там фотография к этой задаче есть?
сейчас
сейчас попробую, но не обещаю
Ответы
Автор ответа:
64
I способ.
В треугольнике АВD АВ=АD (по условию). Следовательно ΔАВD - равнобедренный. ∠В = ∠D как углы при основании равнобедренного треугольника.
Рассмотрим ΔАСD. Он прямоугольный, т.к. АС⊥ВD (по условию).
СD=3,5 - катет; АD=7 - гипотенуза в ΔАСD. Катет СD в два раза короче гипотенузы АD, следовательно он лежит напротив угла в 30°, т.е. ∠САD=30°.
∠D=90°-∠САD=90°-30°=60°.
Ответ: ∠В=∠D=60°.
II способ.
Т.к. АВ=АD, то ΔАВD равнобедренный.
АС - высота, проведенная из вершины равнобедренного треугольника к основанию. Она также является медианой.
ВС=СD. ВD=2·СD=2·3,5=7.
В ΔАВD AD=DВ=ВA=7, следовательно ΔАВD равносторонний.
В равностороннем треугольнике все углы равны 60°. Значит ∠А=∠В=∠D=60°.
Ответ: ∠В=∠D=60°.
Приложения:
Похожие вопросы
Предмет: Химия,
автор: Мозг2016
Предмет: Геометрия,
автор: няяшкааа
Предмет: Математика,
автор: перчик23
Предмет: Математика,
автор: Мудрец123321456654
Предмет: Химия,
автор: Viktoriazzzz