Предмет: Алгебра,
автор: Myasko99
Выразите |sinx-cosx| через a, если sinx+cosx=a.
Ответы
Автор ответа:
2
Решение прицеплено в картинке.
Приложения:
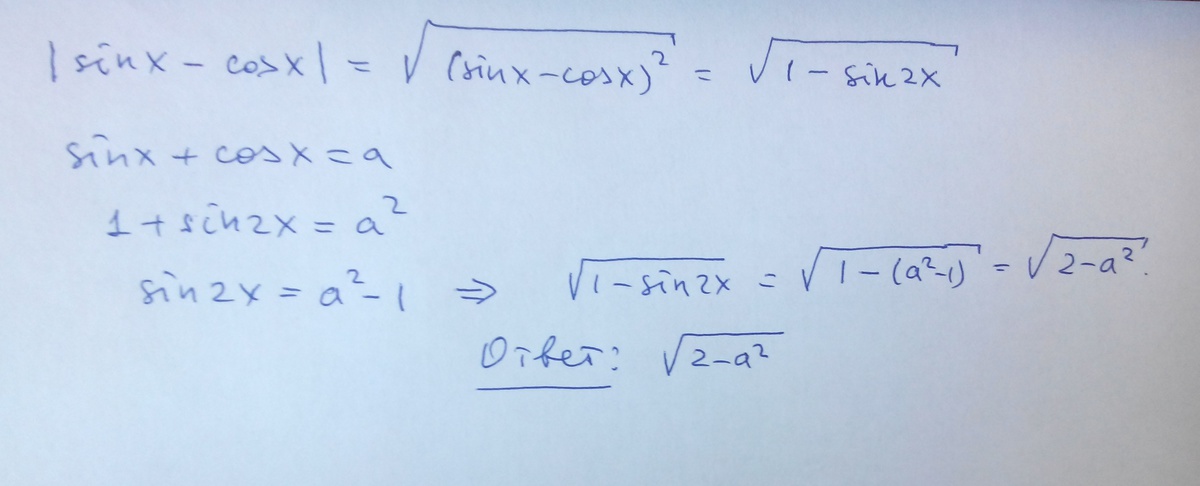
Автор ответа:
1
sinx+cosx=a
sinx+sin(π/2-x)=2sinπ/4cos(x-π/4)=√2cos(x-π/4)=a
cos(x-π/4)=a/√2
sin(x-π/4)=√(1-cos²(x-π/4))²=√(1-a²/2)=√(2-a²)/√2
sinx-cosx=sinx-sinx(π/2-x)=2sin(x-π/4)cosπ/4=√2sin(x-π/4)
|sinx-cosx|=|√2sin(x-π/4)|=√2*√(2-a²)/√2=√(2-a²)
sinx+sin(π/2-x)=2sinπ/4cos(x-π/4)=√2cos(x-π/4)=a
cos(x-π/4)=a/√2
sin(x-π/4)=√(1-cos²(x-π/4))²=√(1-a²/2)=√(2-a²)/√2
sinx-cosx=sinx-sinx(π/2-x)=2sin(x-π/4)cosπ/4=√2sin(x-π/4)
|sinx-cosx|=|√2sin(x-π/4)|=√2*√(2-a²)/√2=√(2-a²)
Похожие вопросы
Предмет: Русский язык,
автор: sapela
Предмет: Биология,
автор: JAM0709
Предмет: Математика,
автор: matveykabutori
Предмет: Математика,
автор: andruskodenis1