Предмет: Математика,
автор: Аноним
нужно доказать тождество.. с ПОЛНЫМ решением...
Приложения:
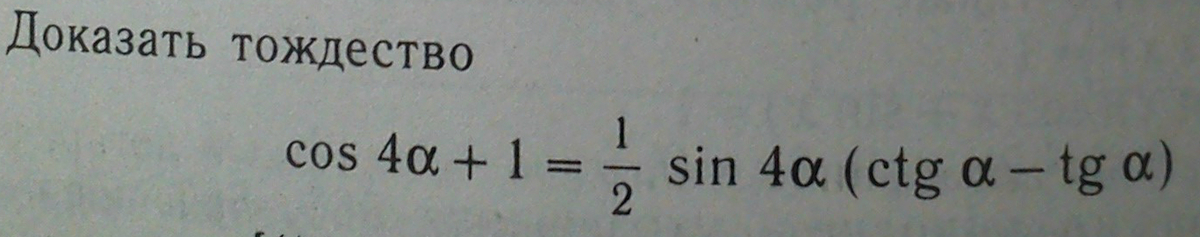
Ответы
Автор ответа:
1
Рассмотрим правую часть:
Сначала посчитаем то, что в скобках:
ctgx - tgx = cosx/sinx - sinx/cosx = (cos^2(x) - sin^2(x))/(sin(x)*cos(x)) =
2*cos(2x)/sin(2x)
Теперь то, что вне скобок:
(1/2) * sin4x = sin(2x)*cos(2x)
перемножаем оба результата, получаем:
2*cos^2(2x)
Теперь левая часть:
cos4x + 1 = 1 + cos^2(2x) - sin^2(2x) = (1 - sin^2(2x)) + cos^2(2x) = 2*cos^2(2x)
Обе части равны, тождество доказано
Сначала посчитаем то, что в скобках:
ctgx - tgx = cosx/sinx - sinx/cosx = (cos^2(x) - sin^2(x))/(sin(x)*cos(x)) =
2*cos(2x)/sin(2x)
Теперь то, что вне скобок:
(1/2) * sin4x = sin(2x)*cos(2x)
перемножаем оба результата, получаем:
2*cos^2(2x)
Теперь левая часть:
cos4x + 1 = 1 + cos^2(2x) - sin^2(2x) = (1 - sin^2(2x)) + cos^2(2x) = 2*cos^2(2x)
Обе части равны, тождество доказано
Похожие вопросы
Предмет: Биология,
автор: ialmiz
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: darsistar
Предмет: Английский язык,
автор: arsen6129
Предмет: Математика,
автор: slavik1412