Question

y=x^2, y=x^1/2 Вычислить площадь фигуры, ограниченной линиями.

Answer 1

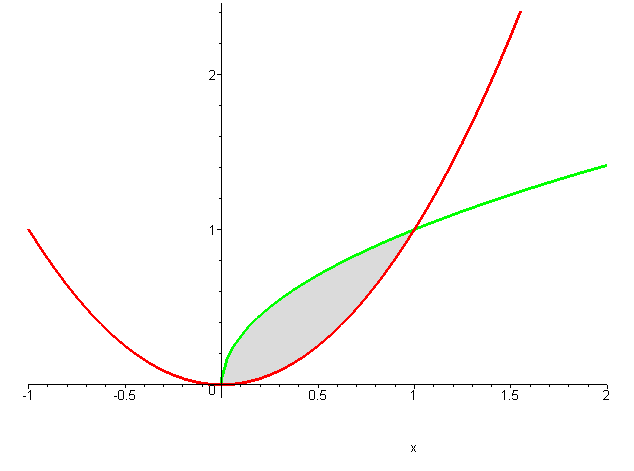
Построим схематически график (см. рис.). Будем искать площадь заштрихованной области.
Слева и справа фигура ограничена точками пересечения графиков. Найдём эти точки (пределы интегрирования):
$x^2=\sqrt x\\x^4=x\\x(x^3-1)=0\\x_1=0,\;x_2=1$.
Найдём площадь фигуры:
$\int\limits_0^1(x^{\frac12}-x^2)dx=\int\limits_0^1x^{\frac12}dx-\int\limits_0^1x^2dx=\left.\left(\frac23x^{\frac32}-\frac13x^3\right)\right|_0^1=\frac23-\frac13-0=\frac13$