Предмет: Алгебра,
автор: parkur11221
Помогите пожалуйста ) извините ,за почерк)
Приложения:
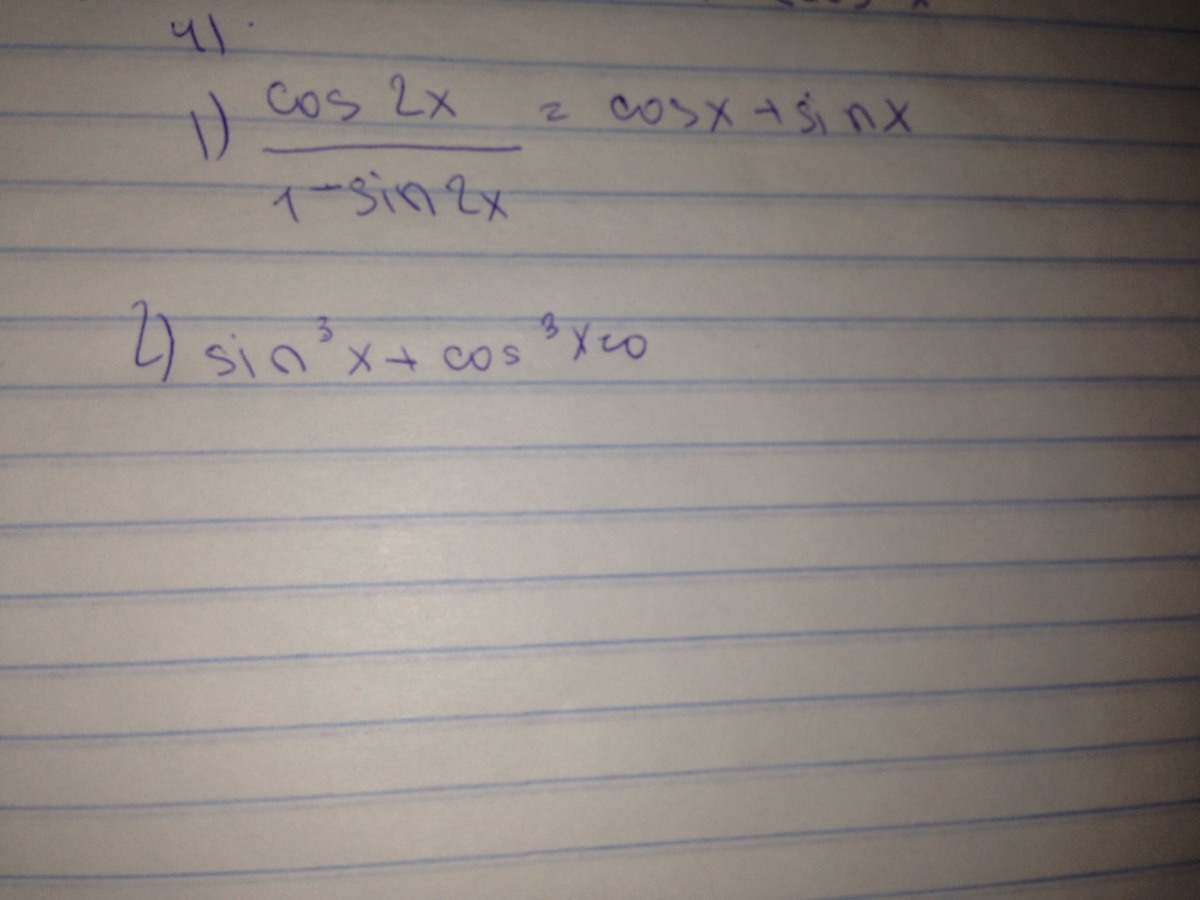
Ответы
Автор ответа:
1
cos x+ sin x=0 |: cos x
tg x=-1
x=-π/4+πn,n ∈ Z
Формула:
Похожие вопросы
Предмет: Русский язык,
автор: Minipesik2007
Предмет: Литература,
автор: kolya134
Предмет: Русский язык,
автор: милана562
Предмет: Қазақ тiлi,
автор: nadiy9
Предмет: Биология,
автор: Аноним