Предмет: Геометрия,
автор: lizatanova
В прямоугольном треугольнике с углом 30 градусов и меньшим катетом 6 см проведены средние линии найдите периметр треугольника образованного средними линиями
Ответы
Автор ответа:
27
cначала найдем стороны большого прямоугольного ΔАВС:
Если один из острых углов 30°, значит другой 60°.
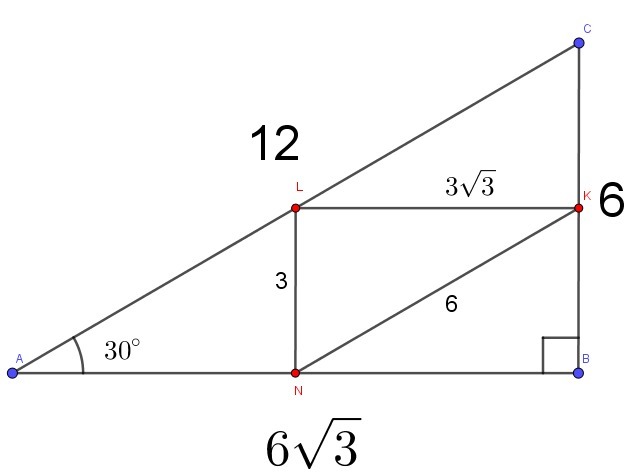
Напротив меньшего угла лежит меньшая сторона, следовательно в нашем случае ВС=6 (см. рисунок)
если на против угла в 30° лежит катет равный 6 см, то гипотенуза будет равна 2*6=12 см; АВ² = 12²-6²=144-36=108.
АВ=√108=6√3
средняя линия в 2 раза меньше основания треугольника, значит: NK=12/2=6см; LN=6/2=3 см; KL=6√3/2=3√3
Р=NK+KL+LN=6+3√(3)+3=9+3√3
Ответ: 9+3√3
Приложения:
Похожие вопросы
Предмет: Биология,
автор: мббббюабсюж
Предмет: Литература,
автор: Оксаночка51
Предмет: Русский язык,
автор: rrrr10
Предмет: Математика,
автор: rusyaewanatali