Предмет: Математика,
автор: xMidx
Помогите пожалуйста
Исследуйте и постройте график функции 
функция четная, имеет 1 максимум
опять ошибся
функция четная, имеет 1 минимум
функция четная, имеет 1 минимум
можно и просто график)
Ответы
Автор ответа:
1
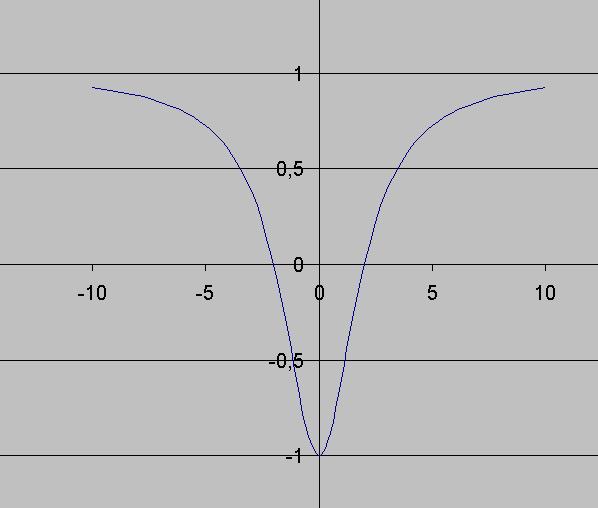
y=(x^2-4)/(x^2+4)=1-8/(x^2+4)
функция четная
y`=16x/(x^2+4)^2
y`=16x/(x^2+4)^2=0 при х=0 - точка экстремума
y``=(16*(x^2+4)^2-16x*2*(x^2+4)*2x)/(x^2+4)^4=
=(16*(x^2+4)-16x*2*2x)/(x^2+4)^3=
=16*(4-3x^2)/(x^2+4)^3
y``(х=0)=16*(4-3*0^2)/(0^2+4)^3=16*4/(4)^3=1/4 >0
значит при х=0 производная меняет знак с - на + и х=0 - точка минимума
y``=0 при х1=2/корень(3) и при х2=-2/корень(3) - точки перегиба
y=1 - горизонтальная асимптота
график прилагается
функция четная
y`=16x/(x^2+4)^2
y`=16x/(x^2+4)^2=0 при х=0 - точка экстремума
y``=(16*(x^2+4)^2-16x*2*(x^2+4)*2x)/(x^2+4)^4=
=(16*(x^2+4)-16x*2*2x)/(x^2+4)^3=
=16*(4-3x^2)/(x^2+4)^3
y``(х=0)=16*(4-3*0^2)/(0^2+4)^3=16*4/(4)^3=1/4 >0
значит при х=0 производная меняет знак с - на + и х=0 - точка минимума
y``=0 при х1=2/корень(3) и при х2=-2/корень(3) - точки перегиба
y=1 - горизонтальная асимптота
график прилагается
Приложения:
Спасибо огромное!!!
Похожие вопросы
Предмет: Математика,
автор: ярик432
Предмет: Химия,
автор: AlexDan5
Предмет: География,
автор: Styx13
Предмет: Геометрия,
автор: smart000001
асимптота у=1
функция четная, имеет 1 минимум и 2 максимума