Предмет: Алгебра,
автор: Velogonschik
Помогите пожалуйста решить эти два примера!
Приложения:
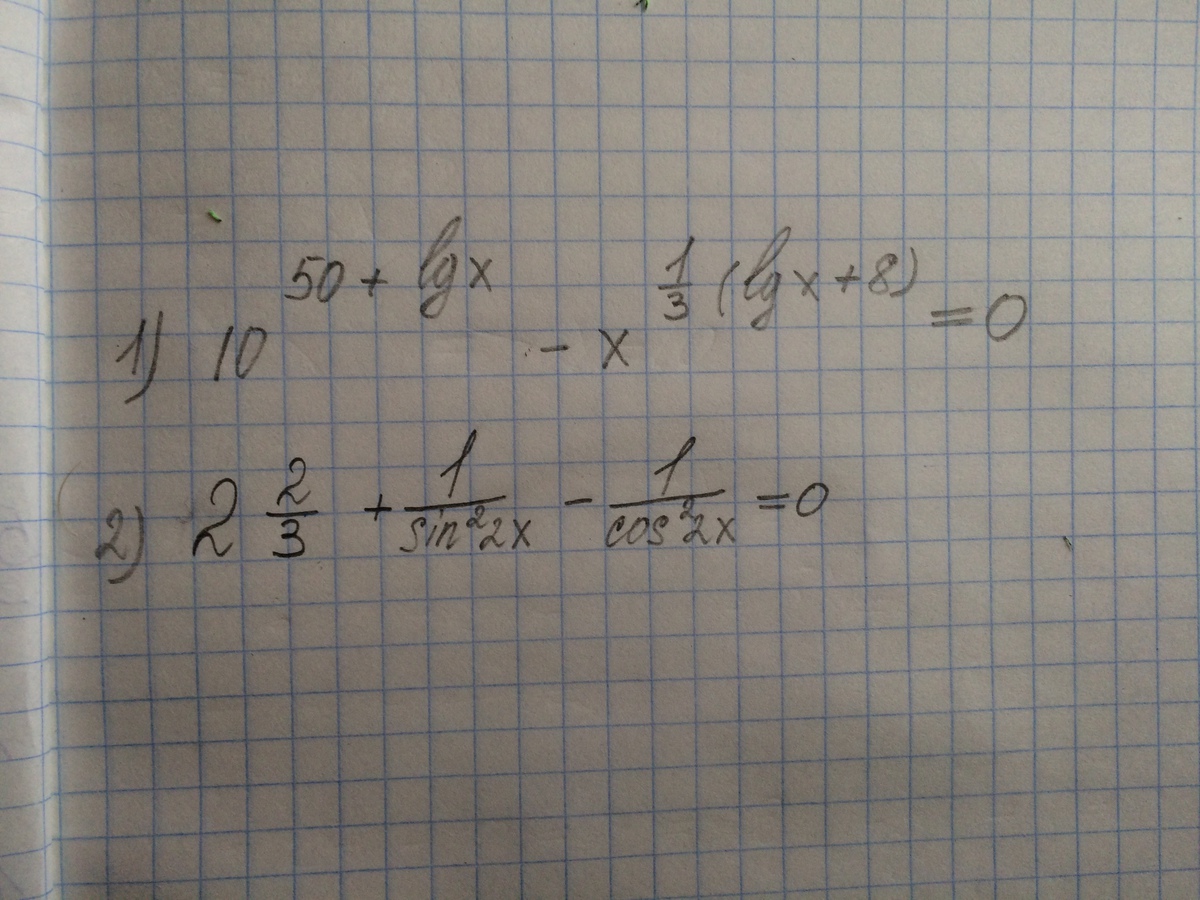
Матов:
перезагрузи страницу если не видн
Ответы
Автор ответа:
1
возьмем с обеих частей
Спасибо) конечно, но я уже решил))
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: Mirasimus
Предмет: Геометрия,
автор: Уникум123
Предмет: Математика,
автор: pasdd12345
Предмет: Математика,
автор: evelina8962