Предмет: Математика,
автор: ysucheninova
Найти площадь фигуры y=x^2+2x, y=x+2
Ответы
Автор ответа:
1
Приложения:
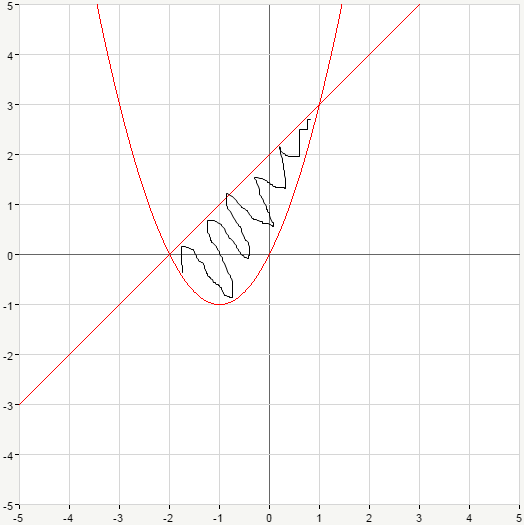
Похожие вопросы
Предмет: Русский язык,
автор: настя7369
Предмет: Английский язык,
автор: melancholyBIOT
Предмет: Алгебра,
автор: Персик571
Предмет: Английский язык,
автор: Аноним