Предмет: Математика,
автор: katyaspiridono
2)Дано уравнение (1-cos2x-sinx)/(cosx-1)=0.
а)Решите уравнение.
б)Укажите его корни, принадлежащие интервалу (5π/2;5π).
Ответы
Автор ответа:
1
a)

Числитель
1 - cos(2x) - sin x=0
1 - (1 - 2sin²x) - sin x = 0
2 sin²x - sin x = 0 ⇔ sin x (2 sin x - 1) = 0
1) 2 sin x - 1 = 0 ⇔ sin x = 1/2 ⇒
x₁ = π/6 + 2πk; x₂ = 5π/6 + 2πm
2) sin x = 0 ⇒ x₃ = πn
Знаменатель
cos x - 1 ≠ 0 ⇔ cos x ≠ 1
x ≠ 2πs, s∈Z ⇒ для x₃ = πn нужно отбросить корни при чётном n
Корни уравнения
x₁ = π/6 + 2πk; x₂ = 5π/6 + 2πm; x₃ = π + 2πn; k,m,n∈Z
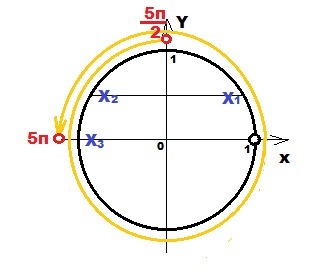
b) Отобрать корни из интервала
(5π/2; 5π) - границы в интервал не входят
(5π/2; 5π) ⇔ (2π + π/2; 4π + π)
x₁ = π/6 + 2πk; попадает в интервал при k=2;
x₁₂ = π/6 + 4π;
x₂ = 5π/6 + 2πm; попадает в интервал дважды - при m=1; m=2
x₂₁ = 5π/6 + 2π; x₂₂ = 5π/6 + 4π;
x₃ = π + 2πn; попадает в интервал при n=1
x₃₁ = π + 2π;
Ответ: в интервале 4 корня:
π/6+4π; 5π/6 + 2π; 5π/6 + 4π; π + 2π;
Числитель
1 - cos(2x) - sin x=0
1 - (1 - 2sin²x) - sin x = 0
2 sin²x - sin x = 0 ⇔ sin x (2 sin x - 1) = 0
1) 2 sin x - 1 = 0 ⇔ sin x = 1/2 ⇒
x₁ = π/6 + 2πk; x₂ = 5π/6 + 2πm
2) sin x = 0 ⇒ x₃ = πn
Знаменатель
cos x - 1 ≠ 0 ⇔ cos x ≠ 1
x ≠ 2πs, s∈Z ⇒ для x₃ = πn нужно отбросить корни при чётном n
Корни уравнения
x₁ = π/6 + 2πk; x₂ = 5π/6 + 2πm; x₃ = π + 2πn; k,m,n∈Z
b) Отобрать корни из интервала
(5π/2; 5π) - границы в интервал не входят
(5π/2; 5π) ⇔ (2π + π/2; 4π + π)
x₁ = π/6 + 2πk; попадает в интервал при k=2;
x₁₂ = π/6 + 4π;
x₂ = 5π/6 + 2πm; попадает в интервал дважды - при m=1; m=2
x₂₁ = 5π/6 + 2π; x₂₂ = 5π/6 + 4π;
x₃ = π + 2πn; попадает в интервал при n=1
x₃₁ = π + 2π;
Ответ: в интервале 4 корня:
π/6+4π; 5π/6 + 2π; 5π/6 + 4π; π + 2π;
Приложения:
Похожие вопросы
Предмет: Математика,
автор: dnd403102
Предмет: Математика,
автор: juliana88
Предмет: Математика,
автор: МастерХ
Предмет: География,
автор: lilollllllll4
Предмет: География,
автор: turanin05