Предмет: Геометрия,
автор: lesyahamathanova
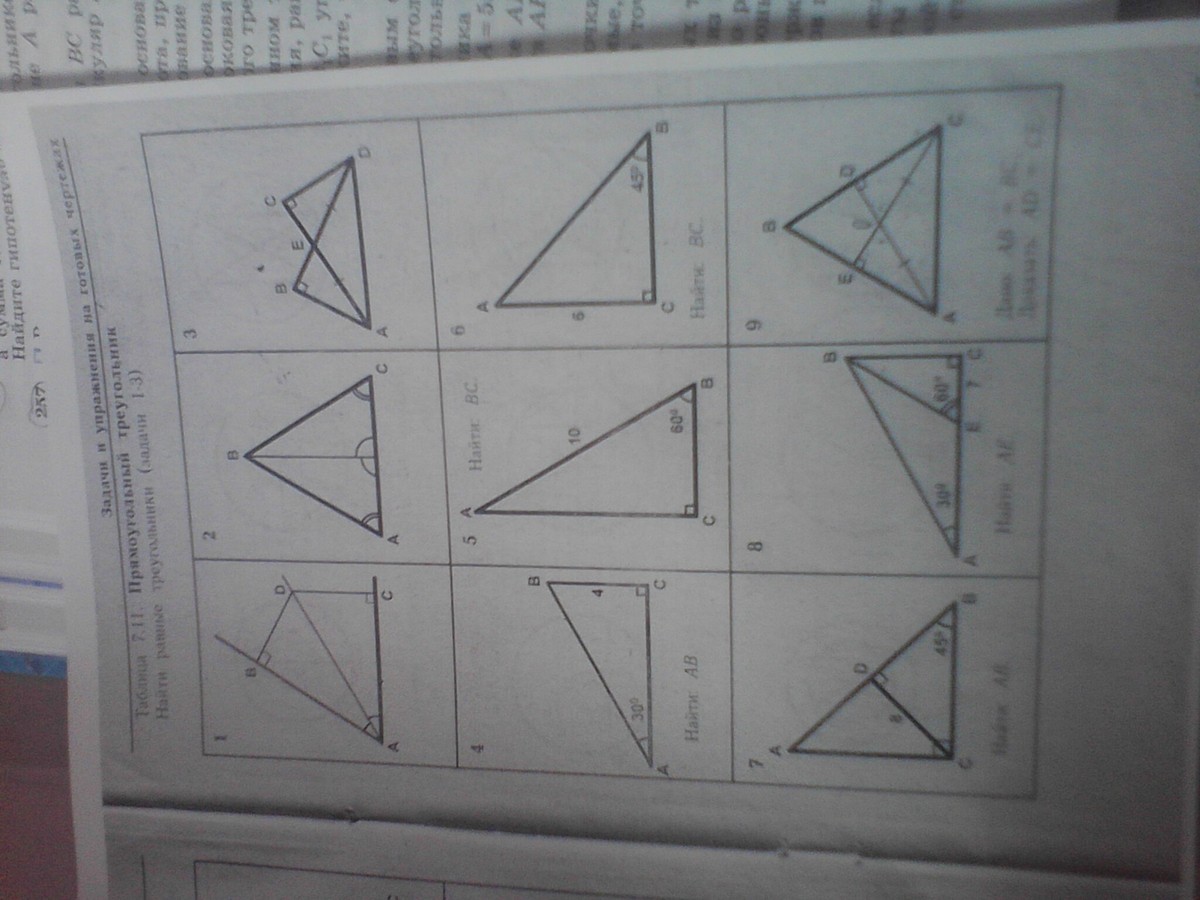
задачи в задачах 1-3 нужно найти равные треугольники с решением помогите решить
Приложения:
Ответы
Автор ответа:
523
1. ∠ABD = ∠ACD = 90° по условию,
∠DAB = ∠DAC по условию,
DA - общая сторона для треугольников DAB и DAC, ⇒
ΔDAB = ΔDAC по гипотенузе и острому углу.
2. ∠BDA = ∠BDC = 180° : 2 = 90°, так как эти углы смежные.
∠BAD = ∠BCD по условию,
сторона BD - общая для треугольников BAD и BDC, ⇒
ΔBAD = ΔBCD по катету и противолежащему острому углу.
3. ∠ABE = ∠DCE = 90°
∠CED = ∠BEA как вертикальные,
ED = EA по условию, ⇒
ΔABE = ΔDCE по гипотенузе и острому углу.
∠ABD = ∠DCA = 90°,
∠EAD = ∠EDA как углы при основании равнобедренного треугольника EAD,
AD - общая сторона для треугольников ABD и DCA, ⇒
ΔABD = ΔDCA по гипотенузе и острому углу.
4. АВ = 2ВС = 2 · 4 = 8, так как катет, лежащий напротив угла в 30°, равен половине гипотенузы.
5. Сумма острых углов прямоугольного треугольника равна 90°. Тогда
∠А = 90° - ∠В = 90° - 60° = 30°.
ВС - катет, лежащий напротив угла в 30°, ⇒
ВС = АВ/2 = 10/2 = 5
6. ∠А = 90° - ∠В = 90° - 45° = 45°, значит ΔАВС равнобедренный,
ВС = АС = 6
7. Прямоугольный треугольник с углом 45° - равнобедренный (доказано в задаче 6), значит высота CD является биссектрисой и медианой.
∠ACD = ∠BCD = 90°/2 = 45°,
тогда и ΔCDB равнобедренный, DB = CD = 8.
AD = DB = 8 (так как CD и медиана), ⇒AB = 16
8. ∠СВЕ = 90° - 60° = 30°
В ΔСВЕ напротив угла в 30° лежит катет ЕС = 7, значит
гипотенуза ВЕ = 2ЕС = 2 · 7 = 14.
∠АВЕ = 60° - ∠ВАЕ = 60° - 30° = 30°, так как внешний угол треугольника (∠ВЕС) равен сумме двух внутренних, на смежных с ним.
Тогда ΔАВЕ равнобедренный, АЕ = ВЕ = 14.
9. Так как ΔАВС равнобедренный, ∠ВАС = ∠ВСА,
∠АЕС = ∠CDA = 90°,
АС - общая сторона для треугольников АЕС и CDA, ⇒
ΔАЕС = ΔCDA по гипотенузе и острому углу.
Значит AD = CE.
∠DAB = ∠DAC по условию,
DA - общая сторона для треугольников DAB и DAC, ⇒
ΔDAB = ΔDAC по гипотенузе и острому углу.
2. ∠BDA = ∠BDC = 180° : 2 = 90°, так как эти углы смежные.
∠BAD = ∠BCD по условию,
сторона BD - общая для треугольников BAD и BDC, ⇒
ΔBAD = ΔBCD по катету и противолежащему острому углу.
3. ∠ABE = ∠DCE = 90°
∠CED = ∠BEA как вертикальные,
ED = EA по условию, ⇒
ΔABE = ΔDCE по гипотенузе и острому углу.
∠ABD = ∠DCA = 90°,
∠EAD = ∠EDA как углы при основании равнобедренного треугольника EAD,
AD - общая сторона для треугольников ABD и DCA, ⇒
ΔABD = ΔDCA по гипотенузе и острому углу.
4. АВ = 2ВС = 2 · 4 = 8, так как катет, лежащий напротив угла в 30°, равен половине гипотенузы.
5. Сумма острых углов прямоугольного треугольника равна 90°. Тогда
∠А = 90° - ∠В = 90° - 60° = 30°.
ВС - катет, лежащий напротив угла в 30°, ⇒
ВС = АВ/2 = 10/2 = 5
6. ∠А = 90° - ∠В = 90° - 45° = 45°, значит ΔАВС равнобедренный,
ВС = АС = 6
7. Прямоугольный треугольник с углом 45° - равнобедренный (доказано в задаче 6), значит высота CD является биссектрисой и медианой.
∠ACD = ∠BCD = 90°/2 = 45°,
тогда и ΔCDB равнобедренный, DB = CD = 8.
AD = DB = 8 (так как CD и медиана), ⇒AB = 16
8. ∠СВЕ = 90° - 60° = 30°
В ΔСВЕ напротив угла в 30° лежит катет ЕС = 7, значит
гипотенуза ВЕ = 2ЕС = 2 · 7 = 14.
∠АВЕ = 60° - ∠ВАЕ = 60° - 30° = 30°, так как внешний угол треугольника (∠ВЕС) равен сумме двух внутренних, на смежных с ним.
Тогда ΔАВЕ равнобедренный, АЕ = ВЕ = 14.
9. Так как ΔАВС равнобедренный, ∠ВАС = ∠ВСА,
∠АЕС = ∠CDA = 90°,
АС - общая сторона для треугольников АЕС и CDA, ⇒
ΔАЕС = ΔCDA по гипотенузе и острому углу.
Значит AD = CE.
Похожие вопросы
Предмет: Математика,
автор: аима3
Предмет: Технология,
автор: nastyaqueen3
Предмет: Английский язык,
автор: stasian04
Предмет: Русский язык,
автор: Fearn22
Предмет: Физика,
автор: ksiaiwiwsj