Question

Задача про двугранный угол, срочно! Желательно с чертежом и развернутым решением.

На гранях двугранного угла взяты две точки, удаленные от ребра двугранного угла на 4 см и 10 см. Известно, что одна из этих точек удалена от второй грани на 5,5 см. Найти расстояние от второй точки до противоположной грани двугранного угла.

Answer 1

Дано: АС=4 см, ВС=10 см; ВН=5,5 см
Найти: АК-?
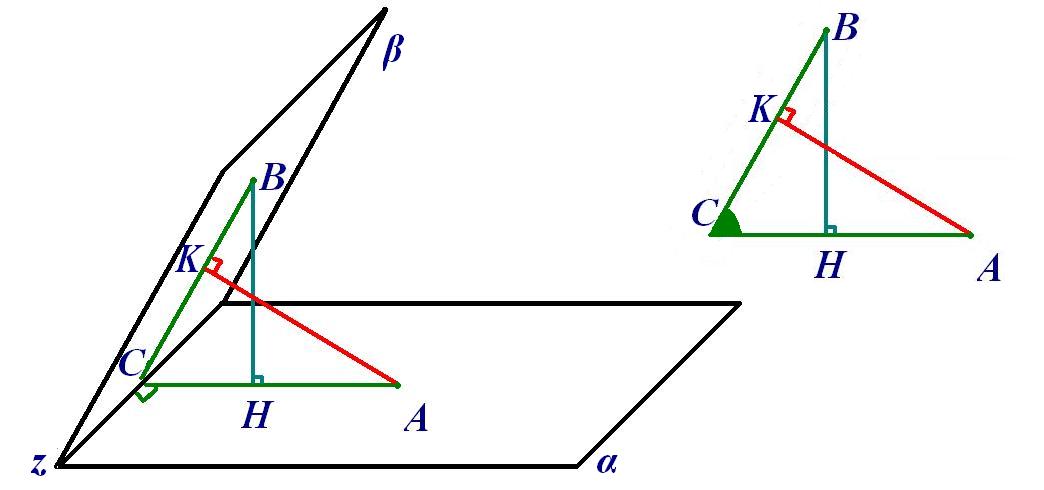
Построение: Так как в условии сказано об удалении точек от ребра двугранного угла, то прямые АС и ВС перпендикулярны к прямой z, содержащей ребро двугранного угла. Удаление точки от другой грани, говорит о том, что ВН перпендикулярно плоскости α и в частности прямой АС, а АК перпендикулярно плоскости β и в частности прямой ВС. Можно спроецировать весь этот рисунок на плоскость, перпендикулярную плоскостям α и β.
Решение: Имеется два треугольника ВСН и АСК с общим углом С. Рассмотрим синус (отношение противолежащего катета к гипотенузе) угла С для двух этих треугольников:
$\sin BCH= \frac{BH}{BC} ; \ \sin ACK= \frac{AK}{AC}$
Левые части этих соотношенйи равны, так как речь идет об одном и том же углы, значит равны и их правые части:
$\frac{BH}{BC}= \frac{AK}{AC}$
Три отрезка из четырех даны по условию, длину четвертого нужно найти:
$AK= \frac{BH\cdot AC}{BC} = \frac{5.5sm\cdot 4sm}{10sm} =2.2sm$
Уточнение: в условии не сказано какая именно из двух точек (удаленная от ребра на 4 см или на 10 см) удалена от второй грани на 5,5 см, но если предположить, что АС=10 см, ВС=4 см, то $\sin BCH=\frac{BH}{BC} = \frac{5.5sm}{4sm} =1.375>1$, чего не может быть.
Ответ: 2,2 см