Предмет: Алгебра,
автор: tolya1511
найти площу фигуры ограниченной линиями y=- x^2 +6x-2 y=x^2-2x+4
Ответы
Автор ответа:
1
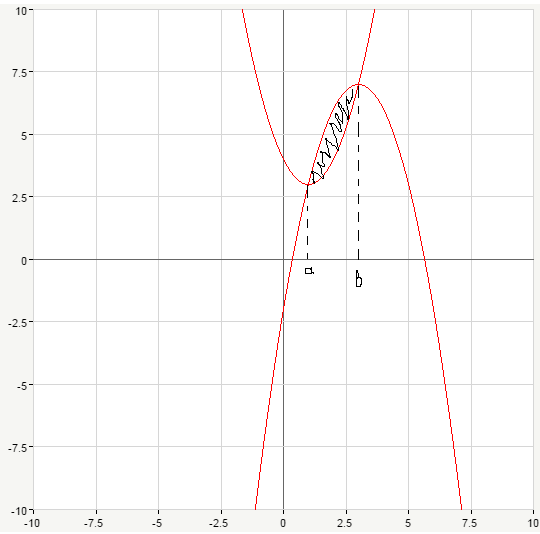
Рисунок во вложении.
Площадь фигуры можно найти по формуле:

Где f(x) - функция ограничивающая фигуру сверху, g(x) - снизу.
a и b - точки пересечения парабол. Найдём их:

a=1, b=3.
Сверху фигура ограничена функцией y=-x²+6x-2, снизу x²-2x+4.
Высчитаем площадь по данной формуле:

Площадь фигуры можно найти по формуле:
Где f(x) - функция ограничивающая фигуру сверху, g(x) - снизу.
a и b - точки пересечения парабол. Найдём их:
a=1, b=3.
Сверху фигура ограничена функцией y=-x²+6x-2, снизу x²-2x+4.
Высчитаем площадь по данной формуле:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: ksy1807
Предмет: Українська мова,
автор: Svetalkllllllkjgd
Предмет: Русский язык,
автор: PROGamerTV1
Предмет: Геометрия,
автор: vertu345
Предмет: Информатика,
автор: maddie12345