Предмет: Алгебра,
автор: sanechik1904
решите неравенство
log5(x+5)+log5(x+1) больше 0
log5( 5 это по оснаванию)
Ответы
Автор ответа:
0
Найдем ОДЗ


Решаем методом интервалов


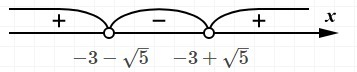
Наносим найденные точки на числовую ось и вычисляем знаки на каждом интервале (смотри рисунок)
Учитываем ОДЗ
Ответ:

Решаем методом интервалов
Наносим найденные точки на числовую ось и вычисляем знаки на каждом интервале (смотри рисунок)
Учитываем ОДЗ
Ответ:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: violettazyrova85
Предмет: Математика,
автор: adis0
Предмет: Алгебра,
автор: dollar176