1)образующая конуса равна 4 sqrt{2}см и наклонена к плоскости основания под углом 45 градусов.найдите площадь полной поверхности конуса 2) сечение цилиндра плоскостью,параллельной оси цилиндра и проходящей от нее на расстоянии,равном половине радиуса цилиндра,представляет собой квадрат.площадь которого равна 108 см в квадрате.Найдите площадь полной поверхнст цилиндра
Ответы
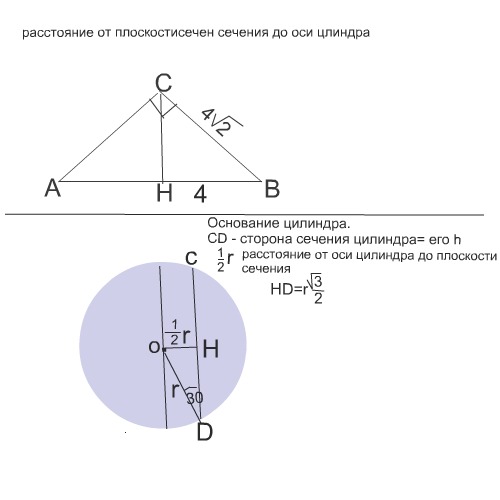
1)
Нарисуем треугольник - осевое сечение конуса. Обозначим его АСВ.
АСВ - равнобедренный прямоугольный треугольник. СВ=d - диагонали квадрата со стороной НВ.
d=а√2
СВ=а√2=4√2, => НВ=4
Площадь полной поверхности конуса равна сумме площади основания и боковой площади.
Sоснов=π r²=π*4²=16π
Sбок= произведению половины длины окружности (2π r):2 на образующую.
Sбок =π r l= π 4*4√2=16√2π
S полная =16π+16√2π=16π(1+√2)
-----------------------------------------------
2)
На рисунке - основание цилиндра.
Треугольник НOD прямоугольный с углом при вершине D=30°, т.к противолежащий катет ОН=половине радиуса r.
НD=ОD*cos(30°)=r(√3):2
CD=cторона сечения=2НD=2r(√3):2=r√3
Площадь сечения - площадь квадрата со стороной CD = 108 см²
CD=√108=6√3
r√3=6√3
r=6
Площадь полной поверхности цилиндра равна сумме площади основания и площади боковой поверхности.
Найдите площадь основания по формуле
S осн=π r²=36π см²
Площадь боковой поверхности цилиндра равна произведению длины окружности на его высоту ( высота равна стороне сечения)
S бок=h* 2 π r=12 π √3
S полн=36π+12 π √3=12π(3+√3)см²