Предмет: Геометрия,
автор: innakar
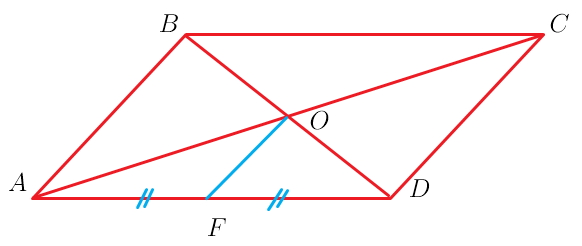
Точка F-середина стороны AD параллелограмма ABCD, диагонали которого пересекаются в точке О. Докажите что треугольники ODFи BDA подобны.
Ответы
Автор ответа:
35
диагонали параллелограмма точкой пересечения делятся пополам,
⇒ О --середина BD
OF соединяет середины сторон треугольника ABD ⇒ является средней линией треугольника ABD и параллельна АВ
углы АВО и FOD равны,
как соответственные при параллельных АВ и OF и секущей BD
угол ADB общий для треугольников ABD и FOD,
следовательно эти треугольники подобны по двум углам))
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Alinaakillova
Предмет: Английский язык,
автор: Dmitriy939
Предмет: Русский язык,
автор: blazefox
Предмет: Русский язык,
автор: nikolya1484
Предмет: Математика,
автор: nika85799