Question

У Крамора, в его книге "Повторяем и систематизируем школьный курс геометрии" 92-ого года издания есть такая задача на с.59:

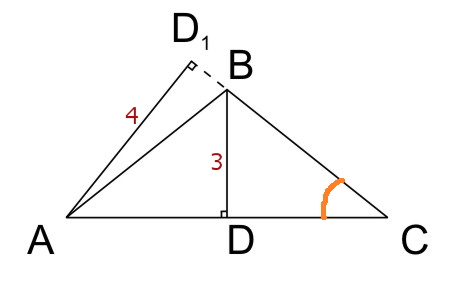
"В равнобедренном треугольнике высота, опущенная на основание равна 3 м, а высота, опущенная на боковую сторону, равна 4 м. Найдите стороны этого треугольника."

я эту задачу уже размещал на "знаниях" и пользователем LFP было найдено два решения: 1) используя свойства подобных треугольников и 2) используя формулу площади треугольника.

вопрос: в рамках школьного курса планиметрии какие ещё, кроме указанных двух, могут быть решения данной задачи?

обоснование вопроса (почему субъективно для меня это важно): сама задача дана в Главе V после § 2 "Теорема Пифагора" (с. 53), темы же, лежащие в основе двух решений, даны: подобия треугольников — в Главе VII § 5 на с. 90; а площади — в Главе X §2 на c. 133. Т.о. не зная этих тем, разбираемых после т. Пифагора, сложновато эту задачу решить (если у неё есть только два указанных решения). Возможны тут три варианта:
а) автор предполагает, всё же, наличие неких знаний из таких тем школьного курса, которые им ещё не изложены, но обязательно необходимы для решения (что, субъективно, не очень мне нравится, поскольку, вот, начал я последовательно изучать данную книгу, а тут оказывается изученного раннее уже не хватает и выясняется, что надо знать нечто, о чём речь будет впереди; это, однако, вряд ли можно ставить в вину автору (в случае целенаправленности данного подхода) поскольку его книга, всё же, не учебник, а именно "повторение...")
б) есть ещё какое-то решение без привлечения тем, разбираемых автором далее
в)данная задача дана после темы т. Пифагора по ошибке...
не знаю, даже, к какому заключению и прийти...

Answer 1

если я не очень Вам надоела, предложу еще вариант)))
-----------------------------------------------т.е. вывод: "есть ещё какое-то решение..."
следуя логике изложения материала в книге Крамора В.С.,
можно обойтись и без формулы площади треугольника,
т.к. в предыдущем параграфе (§ 1) автор дал определение косинуса)))
а это уже начало рассуждений о подобии треугольников)))
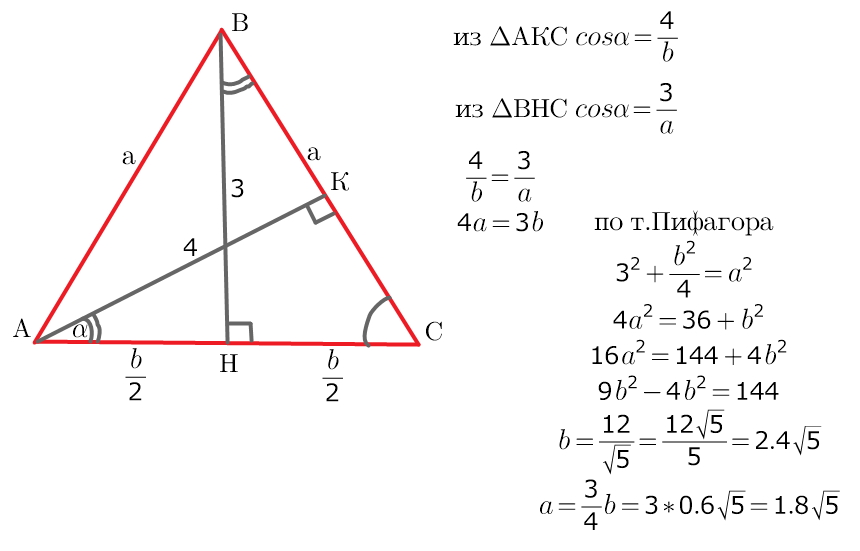
нетрудно заметить, что в получившихся прямоугольных треугольниках есть общий угол, следовательно вторые острые углы этих треугольников равны)))
и можно записать косинусы этих (равных) углов ⇒ и их косинусы тоже будут равны (т.к. "косинус зависит только от величины угла")))
и далее только т.Пифагора...
но на мой вкус, я бы определение косинуса давала вместе с определением синуса)))
и в школьном курсе геометрии формулу площади треугольника проходят гораздо раньше тригонометрических функций)))
как-то так...

Answer 2

... прекрасное, изящное решение (раз в прямоугольных треугольниках один угол общий, значит градусная мера этого угла в этих треугольниках одна и таже, значит и градусные меры вторых острых углов в них одинаковые (!), значит и косинусы равны(!!), а значит и соотношения сторон их равны (!!!)), это именно то, что я и искал, всё тогда встаёт на свои места и задача решается без привлечения не повторенных ещё тем (!)...

Answer 3

... конечно, работа, которую вы проделали может вызвать только восхищение: с такой тщательностью всё это изучили и потратили столько времени! для получения подобной скрупулёзной помощи в математике, обычно, вероятно, принято обращаться к платным репетиторам, вы же проделали её, что называется, безынтересно, что только увеличивает благоговение перед ней!..

Answer 4

значит, моя работа была проделана не зря...