Предмет: Геометрия,
автор: denisdjachin
Найдите объём правильной четырёхугольной пирамиды, боковое ребро которой равно 12см и образует с высотой угол в 30
Ответы
Автор ответа:
0
Найдите объём правильной четырёхугольной пирамиды, боковое ребро которой равно 12 см и образует с высотой угол в 30°.
==========================================================
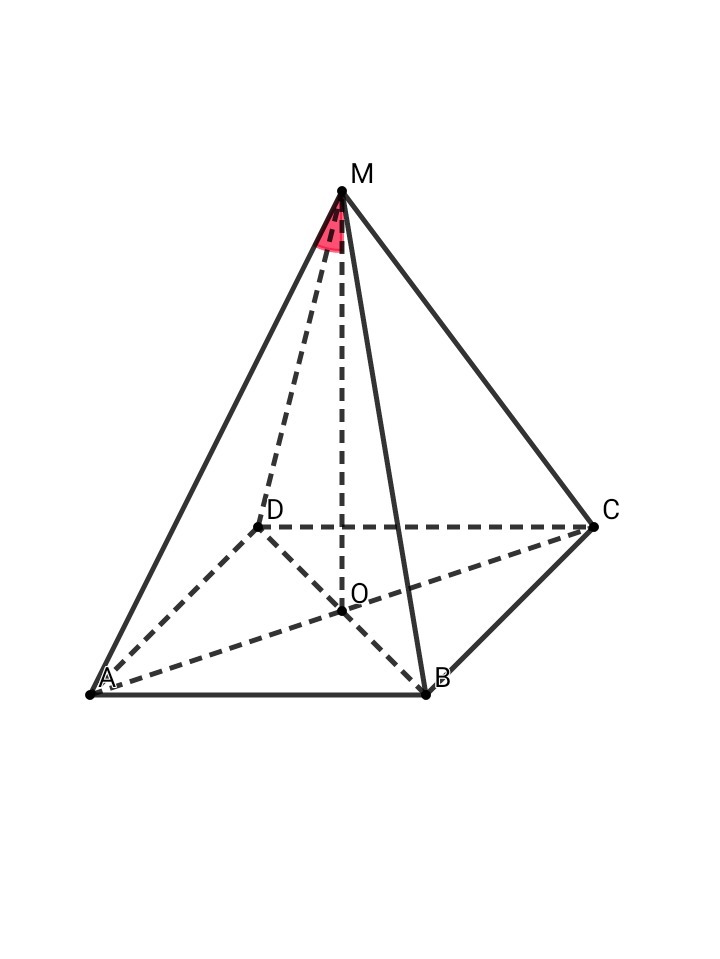
▪В основании правильной четырёхугольной пирамиды лежит квадрат. Вершина такой пирамиды проецируется в точку пересечения диагоналей квадрата. Диагонали квадрата равны, взаимно перпендикулярны и точкой пересечения делятся пополам.
▪Рассмотрим ΔАОМ: ∠АМО = 30° ⇒ катет, лежащий против угла в 30°, равен половине гипотенузы ⇒ АО = АМ/2 = 12/2 = 6 см ⇒ AO = BO = CO = DO = 6 см
По т. Пифагора:
АМ² = АО² + ОМ²
ОМ² = АМ² - АО² = 12² - 6² = 144 - 36 = 108
ОМ = 6√3 см
▪Рассмотрим ΔАОВ: по т. Пифагора
АВ² = АО² + ВО² = 6² + 6² = 36 + 36 = 72
АВ = 6√2 см
V mabcd = S осн. • H / 3 = AB² • MO / 3 = ( 6√2 )² • 6√3 / 3 = 72 • 6√3 / 3 = 144√3 см³
ОТВЕТ: 144√3
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: Valeriapoznak8
Предмет: Английский язык,
автор: Madina8233
Предмет: Алгебра,
автор: evelina858558
Предмет: Физика,
автор: naya987