Предмет: Геометрия,
автор: leraLeraElizarova
В основании пирамиды MABCD лежит квадрат ABCD со стороной, равной 12. Грани MBA и MBC перпендикулярны к плоскости основания. Высота пирамиды равна 5.
Найдите площадь полной поверхности пирамиды
Ответы
Автор ответа:
14
MB - это высота, так как две грани, общей прямой которых она является, перпендикулярны к плоскости основания.
МВС и МВА - два равных прямоугольных треугольника (угол МВС=90° и угол МВА=90° соответственно.
По теореме Пифагора ищем МА
МА²=144+25=169
МА=√169=13
теперь нужно найти MD
проведем диагональ DB, она равна 12√2 (т.к. в основании квадрат)
из прямоугольного треугольника МВD
MD²=(12√2)²+5²=313
MD=√313
осталось найти площадь полной поверхности
по ходу задачи мы выяснили что некоторые грани равны, а именно:
MBC=MBA; MCD=MAD
значит Sполное=Sоснования+2Smbc+2Smcd
Sоснования=12*12=144
S MBC и S MCD найдем по формуле Герона
в первом случае все легко посчитается, получится Smbc=√900=30
во втором посложнее, но все сложится и получится
Smcd=
если сами не сможете, смотрите в приложении как я считала (применяла формулу разности квадратов
теперь все сложим
Sполное=144+2*30+2*78=360
ответ: 360
МВС и МВА - два равных прямоугольных треугольника (угол МВС=90° и угол МВА=90° соответственно.
По теореме Пифагора ищем МА
МА²=144+25=169
МА=√169=13
теперь нужно найти MD
проведем диагональ DB, она равна 12√2 (т.к. в основании квадрат)
из прямоугольного треугольника МВD
MD²=(12√2)²+5²=313
MD=√313
осталось найти площадь полной поверхности
по ходу задачи мы выяснили что некоторые грани равны, а именно:
MBC=MBA; MCD=MAD
значит Sполное=Sоснования+2Smbc+2Smcd
Sоснования=12*12=144
S MBC и S MCD найдем по формуле Герона
в первом случае все легко посчитается, получится Smbc=√900=30
во втором посложнее, но все сложится и получится
Smcd=
если сами не сможете, смотрите в приложении как я считала (применяла формулу разности квадратов
теперь все сложим
Sполное=144+2*30+2*78=360
ответ: 360
Приложения:
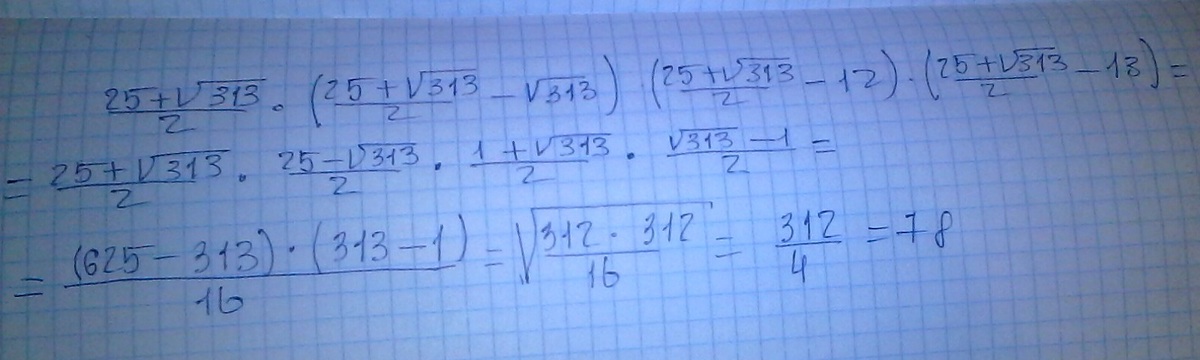
KuOV:
Совет: Решение можно упростить, если найти площадь треугольника МВС как прямоугольного, половина произведения катетов. Легко доказать, что треугольник MAD тоже прямоугольный (АВ - проекция АМ на (АВС), по т. о 3-х перпендикулярах, АМ перпендикулярна AD) и опять половина произведения катетов. Тогда не надо находить MD и не нужны формулы Герона.
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Akejan2008
Предмет: Русский язык,
автор: Bikusia
Предмет: Русский язык,
автор: 12344673
Предмет: Английский язык,
автор: uliagelmelgmailcom
Предмет: Химия,
автор: plombirchik70