Предмет: Алгебра,
автор: lilinab
Ответы
Автор ответа:
0
Приложения:
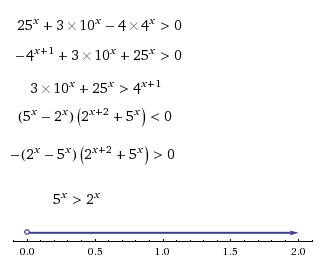
Автор ответа:
0
Пусть , тогда:
1 + 3t -4t^2 >0
4t^2 - 3t - 1 < 0
D = 9 +4*4 = 25
t = (3 +- 5)/8
t1 = 1 t2 = -1/4
показательна функция всегда больше 0, значит:
x > 0
Приложения:

Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Другие предметы,
автор: Аноним
Предмет: Физика,
автор: Fluffymed
Предмет: Биология,
автор: Аноним
Предмет: География,
автор: ahastasia96